【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

参考答案:
【答案】(1)点A的坐标为(-4,0),点B的坐标为(8,0),点C的坐标为(0,6)(2)见解析(3)8或16
【解析】
(1)由OBOC=OCOA=2可得OB﹣OA=4,结合OB=2OA可得出OA、OB的长度,从而得出OC的长度,写出点C的坐标即可;(2)分别求出P、Q两点相遇的时间、Q点到达A点的时间,写出不同的时间范围内,PQ的长度y与时间t的关系式即可;(3)O为P、Q的中点,即OP=OQ,将OP、OQ用含t的式子表示,列方程,解出t,然后画图,由于不确定M点位于x轴上方或者下方,所以进行分类讨论,利用割补法分别求出△CMQ的面积.
(1)∵OB﹣OC=OC﹣OA=2,
∴OB﹣OA=4,
∵OB=2OA,
∴OA=4,
∴OB=8,OC=6,
∴C(0,6);
(2)由(1)知:AB=OA+OB=12,
∵点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,
∴点P运动的时间为t(t>0)秒时,AP=t,BQ=3t,
当P、Q两点相遇时的t的值为:12÷(1+3)=3秒,
∵当点Q到达终点A时,点P、Q均停止运动,
∴t的最大值为12÷3=4秒;
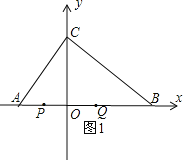
①当0<t≤3时,如图1,
PQ=AB﹣AP﹣QB=12﹣t﹣3t=12﹣4t,
即y=12﹣4t(0<t≤3);
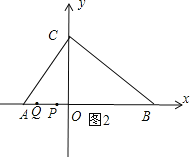
②当3<t≤4时,如图2,
PQ=AP+BQ﹣AB=4t﹣12,
即y=4t﹣12(3<t≤4);
(3)存在t值使点O为PQ中点,
∵点O为PQ中点,
∴0<t≤3,OP=OQ,即OA﹣AP=OB﹣BQ,
∴4﹣t=8﹣3t,解得:t=2,
当t=2时,AP=2,OP=2,OQ=2,PQ=4,PM=PQ=4,
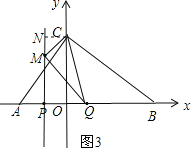
①点M在x轴上方时,如图3,
过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ﹣S△CNM﹣S△PQM,
∴S△CMQ=![]() (CN+PQ)×PN﹣
(CN+PQ)×PN﹣![]() CNMN﹣
CNMN﹣![]() PMPQ
PMPQ
=![]() ×(OP+PQ)×OC﹣
×(OP+PQ)×OC﹣![]() ×OP×(OC﹣PM)﹣
×OP×(OC﹣PM)﹣![]() ×4×4
×4×4
=![]() ×(2+4)×-
×(2+4)×-![]() ×2×(6﹣4) ﹣8
×2×(6﹣4) ﹣8
=18﹣2﹣8=8;
②点M在x轴下方,如图4.过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ+S△PQM-S△CNM,
∴S△CMQ=![]() (CN+PQ)PN+
(CN+PQ)PN+![]() PQPM﹣
PQPM﹣![]() MNCN
MNCN
=![]() ×(OP+PQ)×OC+
×(OP+PQ)×OC+![]() ×4×4﹣
×4×4﹣![]() (OC+PM)OP
(OC+PM)OP
=![]() ×(2+4)×6+8﹣
×(2+4)×6+8﹣![]() ×(6+4)×2
×(6+4)×2
=![]() ×6×6+8﹣
×6×6+8﹣![]() ×10×2
×10×2
=18+8﹣10=16.

∴△CMQ的面积为:8或16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把三角形AE折叠,使点D恰好落在BC边上,设此点为F,若三角形ABF的面积为24,那么CE长度为__________cm2.

-
科目: 来源: 题型:
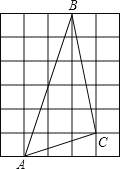
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,若点A(x,
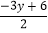 ),点B(2x1,
),点B(2x1,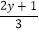 ),点C(z+1,
),点C(z+1,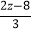 ),已知点A,B关于原点对称,点C在二,四象限平分线上.
),已知点A,B关于原点对称,点C在二,四象限平分线上. (1)求A、B、C点的坐标;
(2)结合A、B、C的坐标,在图中建立平面直角坐标系;
(3)在(2)的条件下,若P为y轴上的一个动点,请直接写出使△PBC周长最小的点P的坐标.
-
科目: 来源: 题型:
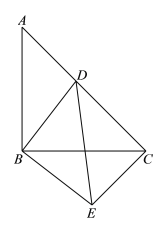
查看答案和解析>>【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
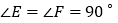 ,
,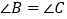 ,
,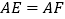 ,给出下列结论:①
,给出下列结论:①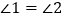 ;②
;②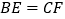 ;③
;③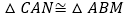 ;④
;④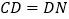 .其中正确的结论是( )
.其中正确的结论是( )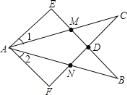
A. ①② B. ②③ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
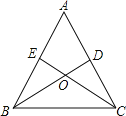
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知将
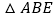 沿
沿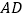 所在直线翻折,点
所在直线翻折,点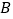 恰好与
恰好与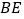 上的点
上的点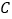 重合,对折边
重合,对折边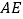 ,折痕也经过点
,折痕也经过点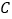 ,则下列说法正确的是( )
,则下列说法正确的是( )①
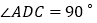 ;
;②
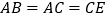 ;
;③
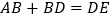 ;
;④
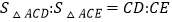 ;
;⑤若
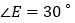 ,则
,则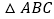 是等边三角形.
是等边三角形.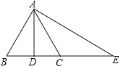
A. 只有①②正确 B. ①②③
C. ①②③④ D. ①②③④⑤
相关试题

