【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

参考答案:
【答案】(1)见解析 (2)45![]() (3)
(3)![]() ;
;![]()
【解析】
(1)①根据A点横坐标及纵坐标的意义解答即可;
②根据函数图象可知,小明出发2小时,爸爸第一次到达度假村,此时小明离家40km,则离度假村的距离可求;
(2)求出小明及小明爸爸的速度,根据题意列方程求出爸爸在返回家的途中与小明相遇时的时间即可解决问题;
(3)由函数图象可知,小明爸爸在返回家的途中与小明相遇之前,不存在相距24km的情况,然后分![]() <t≤3和3<t≤4两种情况,分别列方程求解即可.
<t≤3和3<t≤4两种情况,分别列方程求解即可.
解:(1) ①图中点A表示:爸爸追上小明时,小明出发了![]() 小时,此时离家的距离为30km;
小时,此时离家的距离为30km;
②当爸爸第一次到达度假村后,小明离家40km,则离度假村的距离是20km;
(2)由函数图象可得:小明速度为:60![]() 20km/h,小明爸爸速度为:60
20km/h,小明爸爸速度为:60![]() 1=60km/h,
1=60km/h,
设爸爸在返回家的途中与小明相遇时的时间为t,
由题意得:20t+60(t-1)=60×2,
解得:t=![]() ,
,
20![]() =45km,
=45km,
故爸爸在返回家的途中与小明相遇时,小明离家的距离是45km;
(3)由函数图象可知,小明爸爸在返回家的途中与小明相遇之前,不存在相距24km的情况,
∴当![]() <t≤3时,
<t≤3时,
由题意得:20t-[60×2-60(t-1)]=24,
解得:![]() ,
,
当3<t≤4时,
由题意得:60×3-60(t-1)=24,
解得:![]() ,
,
答:当t的值为![]() 或
或![]() 时,小明与爸爸相距24km.
时,小明与爸爸相距24km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
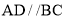 ,
,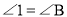 ,
,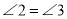 .
.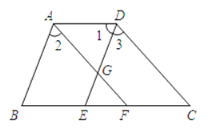
(1)试说明
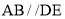 ;
;(2)AF与DC的位置关系如何? 为什么?
下面是本题的解答过程,请补充完整。
解:(1)
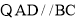 ,(已知)
,(已知)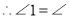 DEC
DEC (_____________________)
(_____________________)又
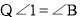 ,(已知)
,(已知)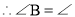 _______,(_____________________)
_______,(_____________________) AB
AB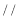 DE
DE (_____________________)
(_____________________)(2)
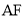 与DC的位置关系是:_______________
与DC的位置关系是:_______________ 理由如下:
理由如下: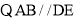 ,(已知)
,(已知)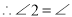 AGD
AGD (_____________________)
(_____________________)又
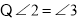 ,(已知)
,(已知)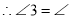 AGD
AGD
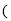 等量代换
等量代换
 _____
_____ ____
____ (_____________________)
(_____________________) -
科目: 来源: 题型:
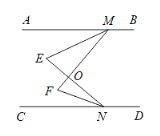
查看答案和解析>>【题目】如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN,MF交于点O.
(1)若∠AMF=50°,∠CNE=40°,∠E= °,∠F= °,∠MON= °;
(2)指出∠E,∠F与∠MON之间存在的等量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在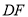 上,点
上,点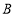 在
在 上,
上,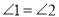 ,
,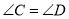 .
.
试说明:
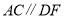 ,将过程补充完整.
,将过程补充完整.解:∵
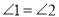 (___________)
(___________)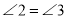 (___________)
(___________)∴
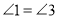 (___________)
(___________)∴________
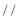 __________(___________)
__________(___________)∴
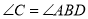 (_____________)
(_____________)又∵
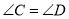 (___________)
(___________)∴
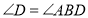 (___________)
(___________)∴
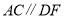 (___________)
(___________) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商店出售了两个进价不同的书包,售价都是42元,其中一个盈利
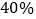 ,另一个亏损
,另一个亏损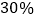 ,则在这次买卖中,商店的盈亏情况是
,则在这次买卖中,商店的盈亏情况是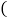
A. 盈利
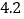 元B. 盈利6元C. 不盈不亏D. 亏损6元
元B. 盈利6元C. 不盈不亏D. 亏损6元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
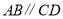 ,
,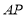 平分
平分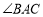 ,
,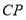 平分
平分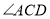 .求
.求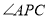 的度数;
的度数;请补全下列解法中的空缺部分.
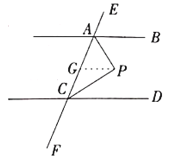
解:过点
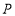 作
作 交
交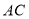 于点
于点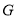
∵
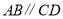 (___________)
(___________)∴_________
 (___________)
(___________)∵
 (___________)
(___________)∴
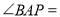 ___________(___________)
___________(___________)且
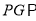 ______________(平行于同一直线的两直线也互相平行)
______________(平行于同一直线的两直线也互相平行)∴
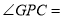 ____________(两直线平行,内错角相等)
____________(两直线平行,内错角相等)∵
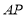 平分
平分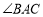 ,
,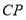 平分
平分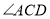 .
.∴
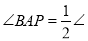 _____________,
_____________,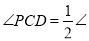 _________________.(___________)
_________________.(___________)∴
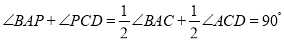 (___________)
(___________)∴
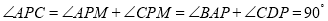
总结:两直线平行时,同旁内角的角平分线_______________.
相关试题

