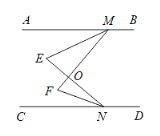
【题目】如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN,MF交于点O.
(1)若∠AMF=50°,∠CNE=40°,∠E= °,∠F= °,∠MON= °;
(2)指出∠E,∠F与∠MON之间存在的等量关系,并证明.
参考答案:
【答案】(1)65;70;90 (2)∠E+∠F=![]() ∠MON;证明见解析
∠MON;证明见解析
【解析】
(1)作EH∥AB,如图,利用平行线的性质得EH∥CD,则∠1=∠AME,∠2=∠CNE,于是得到∠MEN=∠AME+∠CNE,而∠AME=![]() ∠AMF,所以∠MEN=
∠AMF,所以∠MEN=![]() ∠AMF+∠CNE;同理可得∠F=∠AMF+
∠AMF+∠CNE;同理可得∠F=∠AMF+![]() ∠CNE,∠MON=∠AMF+∠CNE;
∠CNE,∠MON=∠AMF+∠CNE;
(2)由(1)可知∠MON=∠AMF+∠CNE,∠E=![]() ∠AMF+∠CNE,∠F=∠AMF+
∠AMF+∠CNE,∠F=∠AMF+![]() ∠CNE,求出∠E+∠F即可得出结论.
∠CNE,求出∠E+∠F即可得出结论.
解:(1)作EH∥AB,如图,
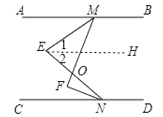
∵AB∥CD,
∴EH∥CD,
∴∠1=∠AME,∠2=∠CNE,
∴∠MEN=∠1+∠2=∠AME+∠CNE,
∵EM是∠AMF的平分线,
∴∠AME=![]() ∠AMF,
∠AMF,
∴∠MEN=![]() ∠AMF+∠CNE=
∠AMF+∠CNE=![]() ×50°+40°=65°;
×50°+40°=65°;
同理可得:∠F=∠AMF+![]() ∠CNE=50°+
∠CNE=50°+![]() ×40°=70°,
×40°=70°,
∠MON=∠AMF+∠CNE=50°+40°=90°,
故答案为:65,70,90;
(2)∠E+∠F=![]() ∠MON
∠MON
证明:由(1)可知:∠MON=∠AMF+∠CNE,∠E=![]() ∠AMF+∠CNE,∠F=∠AMF+
∠AMF+∠CNE,∠F=∠AMF+![]() ∠CNE,
∠CNE,
∴∠E+∠F=![]() (∠AMF+∠CNE),
(∠AMF+∠CNE),
∴∠E+∠span>F=![]() ∠MON.
∠MON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内有∠AOB=60°,∠AOC=40°,OD是∠AOB的平分线,OE是∠AOC的平分线,求∠DOE的度数.(请作图解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, .
.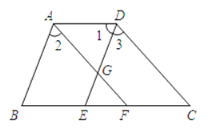
(1)试说明
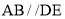 ;
;(2)AF与DC的位置关系如何? 为什么?
下面是本题的解答过程,请补充完整。
解:(1)
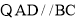 ,(已知)
,(已知)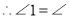 DEC
DEC (_____________________)
(_____________________)又
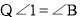 ,(已知)
,(已知)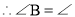 _______,(_____________________)
_______,(_____________________) AB
AB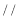 DE
DE (_____________________)
(_____________________)(2)
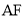 与DC的位置关系是:_______________
与DC的位置关系是:_______________ 理由如下:
理由如下: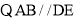 ,(已知)
,(已知)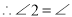 AGD
AGD (_____________________)
(_____________________)又
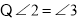 ,(已知)
,(已知)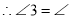 AGD
AGD
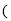 等量代换
等量代换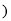
 _____
_____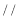 ____
____ (_____________________)
(_____________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明一家到某拓展基地训练,
 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地 如图是他们离家的距离s
如图是他们离家的距离s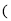 km
km 与小明离家的时问t
与小明离家的时问t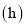 的关系图.
的关系图.(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
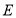 在
在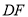 上,点
上,点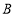 在
在 上,
上,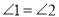 ,
,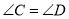 .
.
试说明:
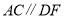 ,将过程补充完整.
,将过程补充完整.解:∵
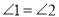 (___________)
(___________)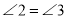 (___________)
(___________)∴
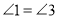 (___________)
(___________)∴________
 __________(___________)
__________(___________)∴
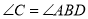 (_____________)
(_____________)又∵
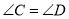 (___________)
(___________)∴
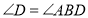 (___________)
(___________)∴
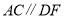 (___________)
(___________) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商店出售了两个进价不同的书包,售价都是42元,其中一个盈利
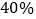 ,另一个亏损
,另一个亏损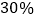 ,则在这次买卖中,商店的盈亏情况是
,则在这次买卖中,商店的盈亏情况是
A. 盈利
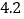 元B. 盈利6元C. 不盈不亏D. 亏损6元
元B. 盈利6元C. 不盈不亏D. 亏损6元
相关试题

