【题目】如图,抛物线经过A(![]() ,0),B(
,0),B(![]() ,0),C(0,2)三点.
,0),C(0,2)三点.
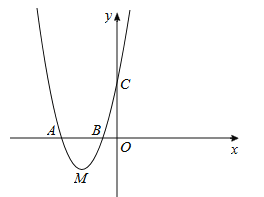
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)D(-1,-1);(3)(
;(2)D(-1,-1);(3)(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得抛物线的解析式;
(2)根据图形的割补法,可得面积的和差,根据二次函数的性质,可得答案;
(3)根据余角的性质,可得∠AMN=∠NKM,根据相似三角形的判定与性质,可得![]() ,根据解方程组,可得H点坐标.
,根据解方程组,可得H点坐标.
试题解析:(1)设抛物线的解析式为![]() ,将A(﹣2,0),B(
,将A(﹣2,0),B(![]() ,0)代入解析式,得:
,0)代入解析式,得: ,解得:
,解得:![]() .∴抛物线的解析式是
.∴抛物线的解析式是![]() ;
;
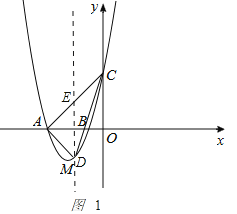
(2)由题意可求得AC的解析式为![]() ,如图1,设D点的坐标为(t,
,如图1,设D点的坐标为(t,![]() ),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=
),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=![]()
![]() ,用h表示点C到线段DE所在直线的距离,
,用h表示点C到线段DE所在直线的距离,
![]() =
=![]() ,∵﹣2<t<0,
,∵﹣2<t<0,
∴当t=﹣1时,△DCA的面积最大,此时D点的坐标为(﹣1,﹣1);
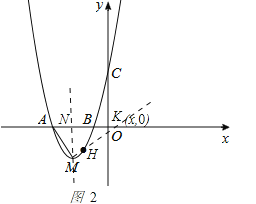
(3)存在点H满足∠AMH=90°,由(1)知M点的坐标为(![]() ,
,![]() ),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴
),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴![]() ,∴
,∴![]() =ANNK,∴
=ANNK,∴![]() ,解得
,解得![]() ,∴K点坐标为(
,∴K点坐标为(![]() ,0),∴直线MK的解析式为
,0),∴直线MK的解析式为![]() ,∴
,∴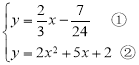 ,把①代入②,化简得
,把①代入②,化简得![]() .△=
.△=![]() ﹣4×48×55=64×4=256>0,∴
﹣4×48×55=64×4=256>0,∴![]() ,
,![]() ,将
,将![]() 代入
代入![]() ,解得
,解得![]() ,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(
,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
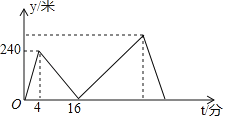
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现:
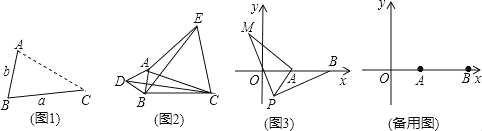
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约
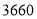 亿
亿 (占总用水量的
(占总用水量的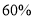 ),工业用水量约为
),工业用水量约为 亿
亿 ,生活用水量具体见下表.
,生活用水量具体见下表.2019-2017年全国生活用水量表(单位:亿
 )
)年份
2009
2010
2011
2012
2013
2014
2015
2016
2017
用水量
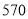
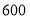
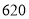
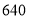
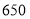

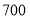
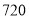

(1)2017年全国总用水量约为 亿
 ,其他用水约为 亿
,其他用水约为 亿 .
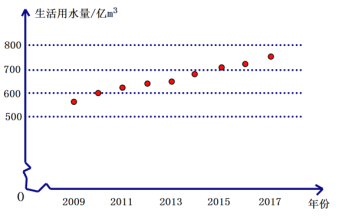
.(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某面粉厂购进标有50千克的面粉10袋,复称时发现误差如下(超过记为正,不足记为负):+0.8 ,+1.6 ,-2.1 ,+0.3 ,-1.6 ,-0.8 ,+0.3 ,+1.6 ,+0.8 ,-0.7
(1)质量最多的是哪袋?它的实际质量是多少?
(2)若质量误差高于0.8千克以上的,则这袋面粉为不合格,这10袋面粉中有哪几袋不合格?不合格率是多少?
(3)问该面粉厂实际收到面粉多少千克?平均质量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中体息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.
(1)直接写出快车速度是 千米/小时.
(2)求快车到达乙地比慢车到达乙地早了多少小时?
(3)求线段BC对应的函数关系式.

相关试题

