【题目】(1)发现:
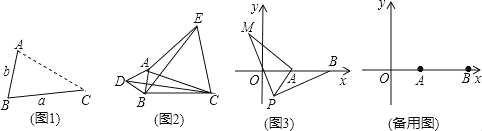
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
参考答案:
【答案】(1) CB的延长线上,a+b;(2)①CD=BE,理由见解析;②4;(3)2![]() +3,P(2﹣
+3,P(2﹣![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2![]() +3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论.
+3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论.
试题解析:(1)∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
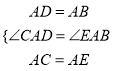 ,
,
∴△CAD≌△EAB(SAS),
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,
∴最大值为BD+BC=AB+BC=4;
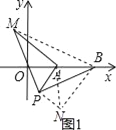
(3)如图1,连接BM,
∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=![]() AP=2
AP=2![]() ,
,
∴最大值为2![]() +3;
+3;
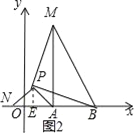
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=![]() ,
,
∴OE=BO﹣AB﹣AE=5﹣3﹣![]() =2﹣
=2﹣![]() ,
,
∴P(2﹣![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
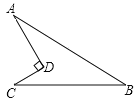
查看答案和解析>>【题目】如图,有一块四边形花圃ABCD,∠ADC=90°,AD=4m,AB=13m,BC=12m,DC=3m,求该花圃的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).
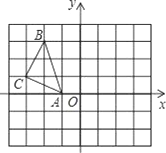
(1)作出△ABC关于x轴对称的 △A1B1C1,并写出B1、C1
两点的坐标:B1: , C1: .
(2)△ABC的面积S△ABC= .
(3)若D点在y轴上运动,求CD+DA的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段能组成一个三角形的是( )
A.4cm,6cm,11cm
B.4cm,5cm,1cm
C.3cm,4cm,5cm
D.2cm,3cm,6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx-10=0的一个根为2,则m=______,另一个根是________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A、点B的坐标分别为(4,0)、(0,3).
(1)求AB的长度.
(2)如图2,若以AB为边在第一象限内作正方形ABCD,求点C的坐标.

(3)在x轴上是否存一点P,使得⊿ABP是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
A.312×104
B.0.312×107
C.3.12×106
D.3.12×107
相关试题

