【题目】某面粉厂购进标有50千克的面粉10袋,复称时发现误差如下(超过记为正,不足记为负):+0.8 ,+1.6 ,-2.1 ,+0.3 ,-1.6 ,-0.8 ,+0.3 ,+1.6 ,+0.8 ,-0.7
(1)质量最多的是哪袋?它的实际质量是多少?
(2)若质量误差高于0.8千克以上的,则这袋面粉为不合格,这10袋面粉中有哪几袋不合格?不合格率是多少?
(3)问该面粉厂实际收到面粉多少千克?平均质量是多少?
参考答案:
【答案】(1)第二袋和第八袋,51.6千克;(2)4袋不合格,不合格率为40%;(3)总质量为500.2千克,平均质量为50.02千克.
【解析】
(1)根据正负数的意义,即可得到答案;
(2)根据误差高于0.8千克以上为不合格,即可得到不合格的数量,然后计算不合格率即可;
(3)通过有理数的运算,可以得到10袋大米的总重量.
解:(1)根据题意,∵第二袋和第八袋为+1.6,
∴质量最多的是第二袋和第八袋,
实际质量为:![]() ;
;
(2)∵质量误差高于0.8千克以上的为不合格,
∴不合格的有:第二袋,第三袋,第五袋,第八袋,共4袋不合格;
∴不合格率为:![]() ;
;
(3)10袋面粉的总质量为:
![]()
=![]() (千克),
(千克),
平均质量为:![]() (千克).
(千克).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现:
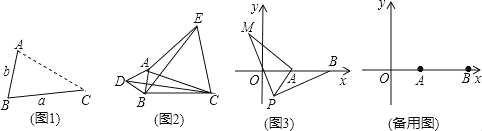
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(
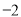 ,0),B(
,0),B(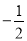 ,0),C(0,2)三点.
,0),C(0,2)三点.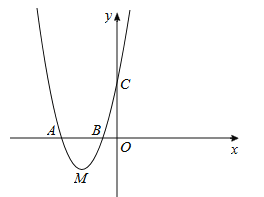
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足
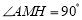 ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约
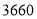 亿
亿 (占总用水量的
(占总用水量的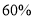 ),工业用水量约为
),工业用水量约为 亿
亿 ,生活用水量具体见下表.
,生活用水量具体见下表.2019-2017年全国生活用水量表(单位:亿
 )
)年份
2009
2010
2011
2012
2013
2014
2015
2016
2017
用水量
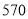
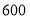
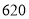
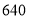
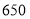

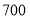
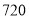

(1)2017年全国总用水量约为 亿
 ,其他用水约为 亿
,其他用水约为 亿 .
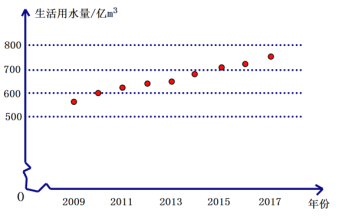
.(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中体息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.
(1)直接写出快车速度是 千米/小时.
(2)求快车到达乙地比慢车到达乙地早了多少小时?
(3)求线段BC对应的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 选举中,人们通常最关心的数据是众数
B. 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大
C. 甲、乙两人在相同条件下各射击10次,他们的平均成绩相同,方差分别为
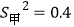 ,
,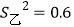 ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定D. 数据3,5,4,1,-2的中位数是4
相关试题

