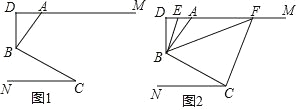
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
参考答案:
【答案】(1)见解析;(2)①见解析,②120°.
【解析】
(1)过B作BG∥CN,依据平行线的性质,以及同角的余角相等,即可得到∠ABD=∠C;
(2)①设∠DBE=∠EBA=x,∠ABF=y,依据∠AFB+∠BCN=∠FBC,即可得到∠AFB=y=∠ABF;
②依据∠CBE=90°,AF∥CN,可得∠ABG+∠CBG=90°,∠BCN+∠AFB+∠BFC+∠BCF=180°,解方程组![]() ,即可得到
,即可得到![]() ,进而得出∠CBE=3x+2y=120°.
,进而得出∠CBE=3x+2y=120°.
(1)如图 1,过 B 作 BG∥CN,
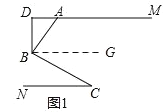
∴∠C=∠CBG
∵AB⊥BC,
∴∠CBG=90°﹣∠ABG,
∴∠C=90°﹣∠ABG,
∵BG∥CN,AM∥CN,
∴AM∥BG,
∴∠DBG=90°=∠D,
∴∠ABD=90°﹣∠ABG,
∴∠ABD=∠C;
(2)①如图 2,设∠DBE=∠EBA=x,则∠BCN=2x,∠FCB=5x, 设∠ABF=y,则∠BFC=1.5y,
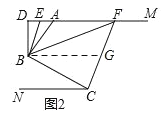
∵BF 平分∠DBC,
∴∠FBC=∠DBF=2x+y,
∵∠AFB+∠BCN=∠FBC,
∴∠AFB+2x=2x+y,
∴∠AFB=y=∠ABF;
②∵∠CBE=90°,AF∥CN,
∴∠ABG+∠CBG=90°,∠BCN+∠AFB+∠BFC+∠BCF=180°,
∴![]()
∴![]()
∴∠CBE=3x+2y=3×30°+2×15°=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小明在解方程组
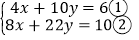 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:
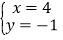 请你解决以下问题:
请你解决以下问题:(1)试用小明的“整体代换”的方法解方程组
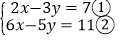
(2)已知 x、y、z,满足
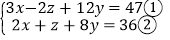 试求 z 的值.
试求 z 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为D,E.
(1)求证:①∠BAD=∠ACE;②BD=AE.
(2)请写出BD,CE,DE三者间的数量关系式,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+1与y轴交于点A1 , 依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
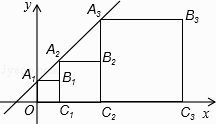
A.(2n﹣1,2n﹣1)
B.(2n﹣1+1,2n﹣1)
C.(2n﹣1,2n﹣1)
D.(2n﹣1,n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是( )
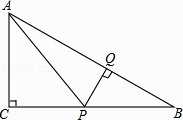
A.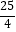
B.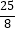
C.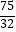
D.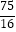
相关试题

