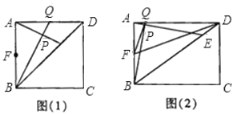
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)证明见解析.
【解析】
(1)①由HL可证明Rt△ABP![]() Rt△EBP;
Rt△EBP;
②证明:过点E作EG⊥AD于点G可得△DEG∽△DBA,可得![]() ,以及△BAQ∽△AGE,可得
,以及△BAQ∽△AGE,可得![]() ,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=
,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=![]() ,代入即可证明:AF2=AQ·AD;
,代入即可证明:AF2=AQ·AD;
(2)延长AE交于CD边于点H,设DH=m,由AB∥CD,可得△DEH∽△BEA,可得AF=2m,由△BAQ∽△ADH,可得![]() 即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
(1)①证明:在正方形ABCD中,∠ABQ=∠DAE.
∵∠ABQ+∠BAP=∠DAE+∠BAP=∠BAD=90°,
∴∠BPA=∠BPE=90°.
在Rt△ABP和Rt△EBP中,
![]() ,
,
∴Rt△ABP![]() Rt△EBP
Rt△EBP
②证明:过点E作EG⊥AD于点G,如图
∴∠GED=∠BAD=90°
∵∠GDE=∠ADB
∴△DEG∽△DBA,
∴![]()
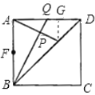
设DG=a,则GE=a,
∴DA=5a,AB=5a,AG=4a.
∵∠ABQ=∠DAE,∠BAQ=∠AGE,
∴△BAQ∽△AGE,
∴![]()
即AQ=![]()
∵F是AB边的中点,
∴![]()
又∵AQ·AD=![]() ,
,
∴AF2=AQ·AD
(2)证明:延长AE交于CD边于点H,设DH=m
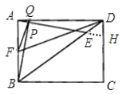
∵四边形ABCD是矩形,
∴AB∥CD,
∴△DEH∽△BEA,
∴![]() 即AB=4m,
即AB=4m,
∴AF=2m
∵∠BAQ=∠APB=90°
∴∠ABQ+∠BAP=∠DAH+∠BAP=90°
∴∠ABQ=∠DAH
∵∠BAQ=∠ADH=90°,∠ABQ=∠DAH
∴△BAQ∽△ADH,,
∴![]() 即AQ·DA=DH·AB=4m2=AF2,
即AQ·DA=DH·AB=4m2=AF2,
∴![]()
又∠FAO=∠DAF,
∴△AFQ∽△ADF,
∴∠AFO=∠ADF.
-
科目: 来源: 题型:
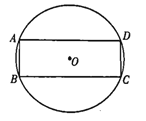
查看答案和解析>>【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
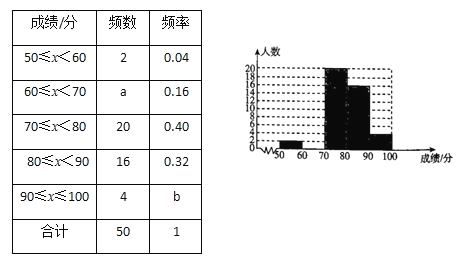
请你根据图表提供的信息,解答下列问题:
(1)求出a,b的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:A.50≤x<60;B.60≤x<80;C.80≤x≤100.若按照这样的分组方式绘制扇形统计图,则其中C组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
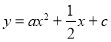 交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
交x轴于A(-4,0),B两点,交y轴于点C(0,-2).(1)求抛物线的解析式;
(2)过点M(m,0)(-4<m<0)且垂直于x轴的直线与抛物线
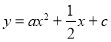 相交于点N,求线段OM+MN的最大值.
相交于点N,求线段OM+MN的最大值.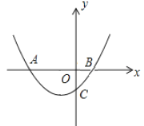
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形ABCD(顶点是网格线的交点)和格点O.

(1)将四边形ABCD先向左平移4个单位长度,再向下平移6个单位长度,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,(点A,B,C,D的对应点分别为点A1,B1,C1,D1);
(2)将四边形ABCD绕点O逆时针旋转90°,得到四边形A2B2C2D2,画出旋转后的四边形A2B2C2D2(点A、B,C,D的对应点分别为点A2,B2,C2,D2);
(3)填空:点C2到A1D1的距离为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知某写字楼AB的正前方有一座信号塔DE,在高为60m的楼顶B处,测得塔尖E处的仰角为30°,从楼底A处向信号塔方向走30m到达C处,测得塔尖E处的仰角为68°,已知点D,C,A在同一水平线上,求信号塔DE的高度.(结果精确到0.1m.参考数据:sin68°≈0.9,cos68°≈0.4,tan 68°≈2.5,
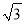 ≈1.7).
≈1.7).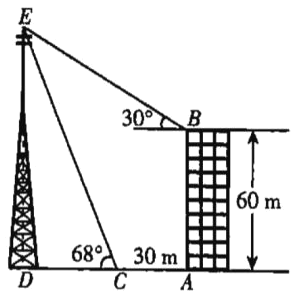
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O为BC上一点,以点O为圆心、OB的长为半径作圆,交BC于点F,交AB于点D,过点D作⊙O的切线,交AC于点E.
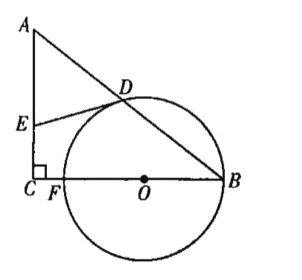
(1)求证:AE=DE;
(2)若
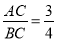 ,CF=2,BF=10,求AD的长.
,CF=2,BF=10,求AD的长.
相关试题

