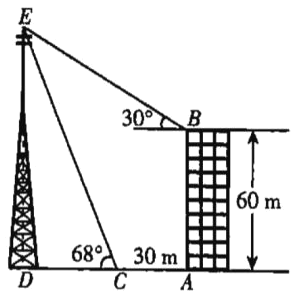
【题目】如图,已知某写字楼AB的正前方有一座信号塔DE,在高为60m的楼顶B处,测得塔尖E处的仰角为30°,从楼底A处向信号塔方向走30m到达C处,测得塔尖E处的仰角为68°,已知点D,C,A在同一水平线上,求信号塔DE的高度.(结果精确到0.1m.参考数据:sin68°≈0.9,cos68°≈0.4,tan 68°≈2.5,![]() ≈1.7).
≈1.7).
参考答案:
【答案】信号塔DE的高度约为101.5m.
【解析】
过点B作BG⊥DE于点G,设CD=xm,在△CDE中,得到DE=CD·tan 68°![]() (m),进而得到EG=DE-GD=(2.5x-60)m;在△EGB中,得到BG=
(m),进而得到EG=DE-GD=(2.5x-60)m;在△EGB中,得到BG=![]() EG=1.7(2.5x-60)m,因为BG=AD,所以1.7(2.5x-60)=x+30,求解即可.
EG=1.7(2.5x-60)m,因为BG=AD,所以1.7(2.5x-60)=x+30,求解即可.
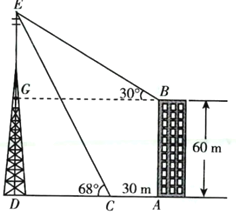
过点B作BG⊥DE于点G.
设CD=xm,
在△CDE中,∠EDC=90°,∠ECD=68°,
则![]() =tan 68°,
=tan 68°,
∴DE=CD·tan 68°![]() (m).
(m).
∵GD=AB=60m,
∴EG=DE-GD=(2.5x-60)m
在△EGB中,∠EGB=90°,∠EBG=30°
则![]() =tan 30°,
=tan 30°,
∴BG=![]() EG=1.7(2.5x-60)m.
EG=1.7(2.5x-60)m.
∴BG=AD,
∴1.7(2.5x-60)=x+30,
解得x=![]()
则DE=2.5×![]() =101.5(m).
=101.5(m).
答:信号塔DE的高度约为101.5m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
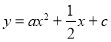 交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
交x轴于A(-4,0),B两点,交y轴于点C(0,-2).(1)求抛物线的解析式;
(2)过点M(m,0)(-4<m<0)且垂直于x轴的直线与抛物线
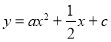 相交于点N,求线段OM+MN的最大值.
相交于点N,求线段OM+MN的最大值.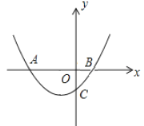
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
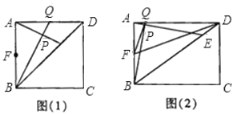
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形ABCD(顶点是网格线的交点)和格点O.

(1)将四边形ABCD先向左平移4个单位长度,再向下平移6个单位长度,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,(点A,B,C,D的对应点分别为点A1,B1,C1,D1);
(2)将四边形ABCD绕点O逆时针旋转90°,得到四边形A2B2C2D2,画出旋转后的四边形A2B2C2D2(点A、B,C,D的对应点分别为点A2,B2,C2,D2);
(3)填空:点C2到A1D1的距离为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O为BC上一点,以点O为圆心、OB的长为半径作圆,交BC于点F,交AB于点D,过点D作⊙O的切线,交AC于点E.
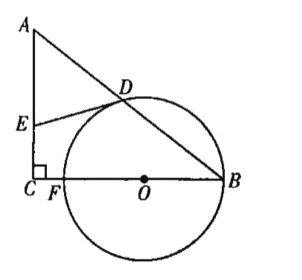
(1)求证:AE=DE;
(2)若
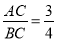 ,CF=2,BF=10,求AD的长.
,CF=2,BF=10,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】电影《我和我的祖国》上映以来好评如潮,某影评平台随机调查了部分观众对这部电影的评分(满分10分),并将调查结果制成了如下不完整的统计图表(表中每组数据不包括最小值,包括最大值):
等级
频数
频率
A等(9.6分~10分)
a
0.7
B等(8.8分~9.6分)
3
0.15
C等(8.2分~8.8分)
b
c
D等(8.2分及以下)
1
0.05
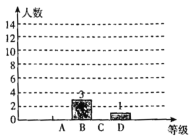
请根据图表信息,解答下列问题:
(1)这次共随机调查了_______名观众,a=______;b=______;c=______;
(2)补全条形统计图;
(3)若某电影院同时上映《我和我的祖国》、《中国机长》和《烈火英雄》,红红和兰兰分别选择其中一部电影观看,求她们选中同一部电影的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2为“互相关联”的抛物线.如图,已知抛物线
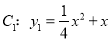 与
与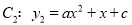 是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).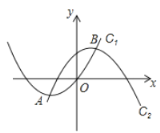
(1)直接写出点A,B的坐标和抛物线C2的解析式.
(2)抛物线C2上是否存在点E,使得△ABE是以AB为直角边的直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.
相关试题

