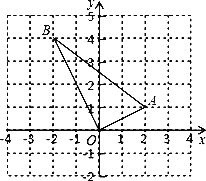
【题目】已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
(1)若点A、B都在一次函数y=kx+b图象上,求k,b的值;
(2)求△OAB的边AB上的中线的长.
参考答案:
【答案】(1)k=﹣![]() ,b=
,b=![]() ;(2)AB边上的中线长为
;(2)AB边上的中线长为![]() .
.
【解析】
(1)由A、B两点的坐标利用待定系数法可求得k、b的值;
(2)由A、B两点到y轴的距离相等可知直线AB与y轴的交点即为线段AB的中点,利用(1)求得的解析式可求得中线的长.
(1)∵点A、B都在一次函数y=kx+b图象上,
∴把(2,1)、(﹣2,4)代入可得![]() ,解得
,解得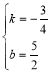 ,
,
∴k=﹣![]() ,b=
,b=![]() ;
;
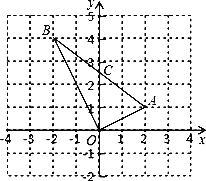
(2)如图,设直线AB交y轴于点C,
∵A(2,1)、B(﹣2,4),
∴C点为线段AB的中点,
由(1)可知直线AB的解析式为y=﹣![]() x+
x+![]() ,
,
令x=0可得y=![]() ,
,
∴OC=![]() ,即AB边上的中线长为
,即AB边上的中线长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
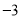
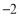
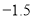
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂现有
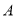 种原料
种原料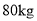 ,
,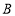 种原料
种原料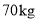 ,现计划用这两种原料生产
,现计划用这两种原料生产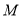 ,
,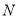 两个品种的饮料,已知生产每千克
两个品种的饮料,已知生产每千克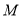 品种的饮料需要
品种的饮料需要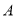 种原料
种原料 ,
,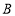 种原料
种原料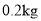 ,可获利
,可获利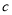 元,生产每千克
元,生产每千克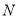 品种的饮料只需要
品种的饮料只需要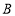 种原料
种原料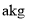 ,可获利3千元,两种原料正好用完.
,可获利3千元,两种原料正好用完.(1)生产
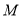 品种的饮料________千克.
品种的饮料________千克.(2)生产
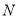 品种的饮料使用
品种的饮料使用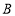 种原料多少千克?
种原料多少千克?(3)该厂共获利多少元?(用含
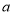 ,
,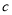 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中有两条直线y=﹣2x+3和y=3x﹣2.
(1)确定这两条直线交点所在的象限,并说明理由;
(2)求两直线与坐标轴正半轴围成的四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①、②、③行第n个数分别为 ; ; .
(2)取每行数的第九个数,计算这三个数的和.
-
科目: 来源: 题型:
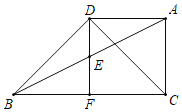
查看答案和解析>>【题目】如图:在△ABC中,点E,F分别是BA,BC边的中点,过点A作AD∥BC交FE的延长线于点D,连接DB,DC.
(1)求证:四边形ADFC是平行四边形;
(2)若∠BDC=90°,求证:CD平分∠ACB;
(3)在(2)的条件下,若BD=DC=6,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB
(2)已知AB=4
 ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.
相关试题

