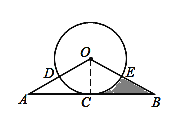
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB
(2)已知AB=4![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)首先连接OC,可得OC⊥AB,然后根据圆心角、弧、弦、弦心距的关系,由弧CD=弧CE,可得∠AOC=∠BOC,进而得出∠A=∠B,利用等角对等边即可证明出结论;
(2)根据(1)可得BC的长,从而得出OC的长,然后根据三角形和扇形的面积计算可得出△BOC和扇形OCE的面积,再两部分作差即可求出阴影部分的面积.
详解:(1) 连接OC,
![]() 与⊙O相切于点C,
与⊙O相切于点C,
![]() ∠ACO=90°,
∠ACO=90°,
∴弧CD=弧CE
![]() ∠AOC=∠BOC,
∠AOC=∠BOC,
![]() ∠A=∠B,
∠A=∠B,
![]() OA=OB,
OA=OB,
(2 )由(1)可以知道: ![]() OAB是等腰三角形,
OAB是等腰三角形,
![]()
![]() ,
,
![]() sin∠COB=
sin∠COB=![]() ,
,
![]() ∠COB=60°,
∠COB=60°,
![]() ∠B=30°,
∠B=30°,
![]()
![]() ,
,
![]() 扇形OCE的面积为:
扇形OCE的面积为:![]() ,
,
![]() OCB的面积为:
OCB的面积为:![]() ,
,
![]() S阴影=
S阴影=![]() .
.
-
科目: 来源: 题型:
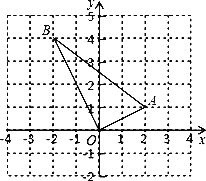
查看答案和解析>>【题目】已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
(1)若点A、B都在一次函数y=kx+b图象上,求k,b的值;
(2)求△OAB的边AB上的中线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①、②、③行第n个数分别为 ; ; .
(2)取每行数的第九个数,计算这三个数的和.
-
科目: 来源: 题型:
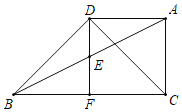
查看答案和解析>>【题目】如图:在△ABC中,点E,F分别是BA,BC边的中点,过点A作AD∥BC交FE的延长线于点D,连接DB,DC.
(1)求证:四边形ADFC是平行四边形;
(2)若∠BDC=90°,求证:CD平分∠ACB;
(3)在(2)的条件下,若BD=DC=6,求AB的长.
-
科目: 来源: 题型:
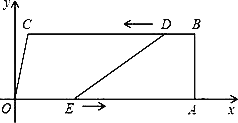
查看答案和解析>>【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
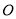 是坐标原点,点A(2,5)在反比例函数
是坐标原点,点A(2,5)在反比例函数 的图象上.一次函数
的图象上.一次函数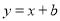 的图象过点A,且与反比例函数图象的另一交点为B.
的图象过点A,且与反比例函数图象的另一交点为B.(1)求
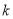 和
和 的值;
的值; (2)设反比例函数值为
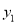 ,一次函数值为
,一次函数值为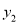 ,求
,求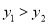 时
时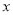 的取值范围.
的取值范围.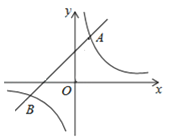
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数
 ,
, ,
, 在数轴上的位置如下图所示:
在数轴上的位置如下图所示:
(1)若
 ,求
,求 的值.
的值.(2)若
 ,
, ,
, ,且
,且 ,
, ,
, 对应的点分别为
对应的点分别为 ,
, ,
, ,问在数轴上是否存在一点
,问在数轴上是否存在一点 ,使
,使 与
与 的距离是
的距离是 与
与 的距离的3倍.若存在,请求出
的距离的3倍.若存在,请求出 点对应的有理数;若不存在,请说明理由.
点对应的有理数;若不存在,请说明理由.
相关试题

