【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
参考答案:
【答案】(1)5.5千克;(2)超过8千克;(3)1422元.
【解析】
(1)根据最大数25+2.5减最小数25+(-3),可得答案;
(2)根据有理数的加法-3×1+(-2)×4+(-1.5)×2+0×3+1×2+2.5×8,计算结果可得答案;
(3)根据有理数的加法,可得总重量,根据单价乘以数量,可得答案.
解:(1)最重的一筐比最轻的一筐多重2.5-(-3)=2.5+3=5.5(千克),
答:20筐白菜中,最重的一筐比最轻的一筐多重5.5千克;
(2)-3×1+(-2)×4+(-1.5)×2+0×3+1×2+2.5×8=8(千克),
答:20筐白菜总计超过8千克;
(3)(25×20+8)×2.8=508×2.8≈1422(元),
答:白菜每千克售价2.8元,则出售这20筐白菜可卖1422元.
-
科目: 来源: 题型:
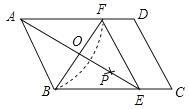
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
 BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
-
科目: 来源: 题型:
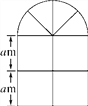
查看答案和解析>>【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂现有
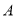 种原料
种原料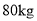 ,
,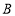 种原料
种原料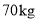 ,现计划用这两种原料生产
,现计划用这两种原料生产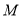 ,
,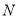 两个品种的饮料,已知生产每千克
两个品种的饮料,已知生产每千克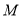 品种的饮料需要
品种的饮料需要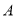 种原料
种原料 ,
,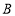 种原料
种原料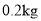 ,可获利
,可获利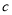 元,生产每千克
元,生产每千克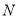 品种的饮料只需要
品种的饮料只需要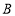 种原料
种原料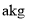 ,可获利3千元,两种原料正好用完.
,可获利3千元,两种原料正好用完.(1)生产
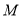 品种的饮料________千克.
品种的饮料________千克.(2)生产
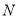 品种的饮料使用
品种的饮料使用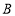 种原料多少千克?
种原料多少千克?(3)该厂共获利多少元?(用含
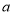 ,
,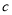 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中有两条直线y=﹣2x+3和y=3x﹣2.
(1)确定这两条直线交点所在的象限,并说明理由;
(2)求两直线与坐标轴正半轴围成的四边形的面积.
-
科目: 来源: 题型:
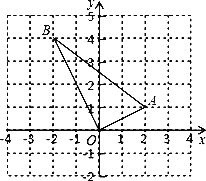
查看答案和解析>>【题目】已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
(1)若点A、B都在一次函数y=kx+b图象上,求k,b的值;
(2)求△OAB的边AB上的中线的长.
相关试题

