【题目】已知:在平面直角坐标系中有两条直线y=﹣2x+3和y=3x﹣2.
(1)确定这两条直线交点所在的象限,并说明理由;
(2)求两直线与坐标轴正半轴围成的四边形的面积.
参考答案:
【答案】(1)两直线交点坐标为(1,1),在第一象限;(2)![]() .
.
【解析】
(1)联立两直线解析式成方程组,解方程组即可求出交点坐标,进而即可得出交点所在的象限;
(2)令直线y=﹣2x+3与x、y轴分别交于点A、B,直线y=3x﹣2与x、y轴分别交于点C、D,两直线交点为E,由直线AB、CD的解析式即可求出点A、B、C的坐标,利用分割图形求面积法结合三角形的面积公式即可求出两直线与坐标轴正半轴围成的四边形的面积.
(1)联立两直线解析式得:![]() ,
,
解得:![]() ,
,
∴两直线交点坐标为(1,1),在第一象限.
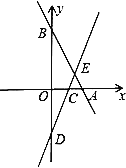
(2)令直线y=﹣2x+3与x、y轴分别交于点A、B,直线y=3x﹣2与x、y轴分别交于点C、D,两直线交点为E,如图所示.
令y=﹣2x+3中x=0,则y=3,
∴B(0,3);
令y=﹣2x+3中y=0,则x=![]() ,
,
∴A(![]() ,0).
,0).
令y=3x﹣2中y=0,则x=![]() ,
,
∴C(![]() ,0).
,0).
∵E(1,1),
∴S四边形OCEB=S△AOB﹣S△ACE=![]() OAOB﹣
OAOB﹣![]() ACyE=
ACyE=![]() ×
×![]() ×3﹣
×3﹣![]() ×(
×(![]() ﹣
﹣![]() )×1=
)×1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
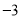
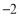
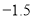
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂现有
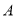 种原料
种原料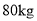 ,
,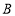 种原料
种原料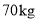 ,现计划用这两种原料生产
,现计划用这两种原料生产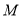 ,
,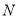 两个品种的饮料,已知生产每千克
两个品种的饮料,已知生产每千克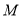 品种的饮料需要
品种的饮料需要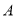 种原料
种原料 ,
,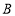 种原料
种原料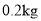 ,可获利
,可获利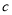 元,生产每千克
元,生产每千克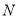 品种的饮料只需要
品种的饮料只需要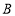 种原料
种原料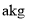 ,可获利3千元,两种原料正好用完.
,可获利3千元,两种原料正好用完.(1)生产
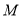 品种的饮料________千克.
品种的饮料________千克.(2)生产
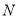 品种的饮料使用
品种的饮料使用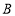 种原料多少千克?
种原料多少千克?(3)该厂共获利多少元?(用含
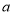 ,
,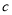 的式子表示)
的式子表示) -
科目: 来源: 题型:
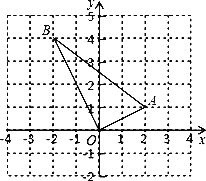
查看答案和解析>>【题目】已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
(1)若点A、B都在一次函数y=kx+b图象上,求k,b的值;
(2)求△OAB的边AB上的中线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①、②、③行第n个数分别为 ; ; .
(2)取每行数的第九个数,计算这三个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,点E,F分别是BA,BC边的中点,过点A作AD∥BC交FE的延长线于点D,连接DB,DC.
(1)求证:四边形ADFC是平行四边形;
(2)若∠BDC=90°,求证:CD平分∠ACB;
(3)在(2)的条件下,若BD=DC=6,求AB的长.
相关试题

