【题目】小敏思考解决如下问题:
原题:如图1,点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,求证:
,求证:![]() .
.
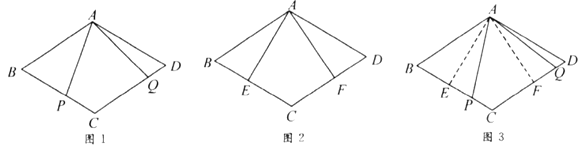
(1)小敏进行探索,若将点![]() ,
,![]() 的位置特殊化:把
的位置特殊化:把![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,使
,使![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,如图2,此时她证明了
上,如图2,此时她证明了![]() .请你证明.
.请你证明.
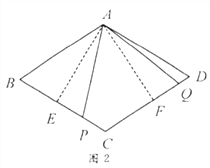
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .请你继续完成原题的证明.
.请你继续完成原题的证明.
(3)如果在原题中添加条件:![]() ,
,![]() ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)见解析
【解析】(1)证明![]() ,即可求证
,即可求证![]() .
.
(2)如图2,![]() ,即可求证
,即可求证![]() .
.
(3)不唯一.
【解答】(1)如图1,
在菱形![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
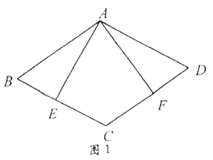
(2)如图2,由(1),∵![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)不唯一,举例如下:
层次1:①求![]() 的度数.答案:
的度数.答案:![]() .
.
②分别求![]() ,
,![]() 的度数.答案:
的度数.答案:![]() .
.
③求菱形![]() 的周长.答案:16.
的周长.答案:16.
④分别求![]() ,
,![]() ,
,![]() 的长.答案:4,4,4.
的长.答案:4,4,4.
层次2:①求![]() 的值.答案:4.
的值.答案:4.
②求![]() 的值.答案:4.
的值.答案:4.
③求![]() 的值.答案:
的值.答案:![]() .
.
层次3:①求四边形![]() 的面积.答案:
的面积.答案:![]() .
.
②求![]() 与
与![]() 的面积和.答案:
的面积和.答案:![]() .
.
③求四边形![]() 周长的最小值.答案:
周长的最小值.答案:![]() .
.
④求![]() 中点运动的路径长.答案:
中点运动的路径长.答案:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用
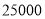 元购进
元购进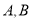 两种新型护服台灯共
两种新型护服台灯共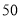 盏,这两种台灯的进价、标价如下表所示:
盏,这两种台灯的进价、标价如下表所示:价格
 类型
类型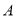 型
型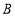 型
型进价(元/盏)
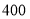
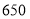
标价(元/盏)
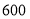
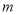
(1)
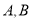 两种新型护眼台灯分别购进多少盏?
两种新型护眼台灯分别购进多少盏?(2)若
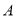 型护眼灯按标价的
型护眼灯按标价的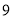 折出售,
折出售,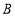 型护眼灯按标价的
型护眼灯按标价的 折出售,那么这批台灯全部售完后,商场共获利
折出售,那么这批台灯全部售完后,商场共获利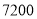 元,请求出表格中
元,请求出表格中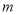 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量
 (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程 (千米)的函数图象.
(千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求
 关于
关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
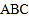 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
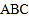 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
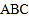 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形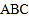 中,设
中,设 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索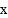 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,3),B(5,1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
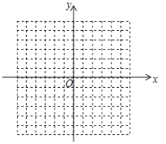
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于x轴对称的△A′B′C′,并写出△A′B′C′各顶点坐标;
(3)在x轴上找一点P,使PA+PB的值最小。请画出点P,并求出点P坐标。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 平面直角坐标系的原点,三角形
平面直角坐标系的原点,三角形 中,
中, ,顶点
,顶点 的坐标分别为
的坐标分别为 ,且
,且 .
.
(1)求三角形
 的面积;
的面积;(2)动点
 从点
从点 出发沿射线
出发沿射线 方向以每秒
方向以每秒 个单位长度的速度运动,设点
个单位长度的速度运动,设点 的运动时间为t秒.连接
的运动时间为t秒.连接 ,请用含t的式子表示三角形
,请用含t的式子表示三角形 的面积;
的面积;(3)在(2)的条件下,当三角形
 的面积为
的面积为 时,直线
时,直线 与
与 轴相交于点
轴相交于点 ,求点
,求点 的坐标
的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进了一批
 、
、 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:类型
进购数量(个)
进价(元/个)
售价(元/个)
 型
型20
1800
2300
 型
型40
1500
?
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则
 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
相关试题

