【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
参考答案:
【答案】至少是2050元.
【解析】
设购进B型智能扫地机器人的单价为x,根据总利润=单台利润×购进数量结合总利润不少于32000元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其中最小的整数即可得出结论.
设购进B型智能扫地机器人的单价为x,则根据题意可得:
![]()
![]()
![]()
![]()
故![]() 型智能扫地机器人的销售单价至少是2050元.
型智能扫地机器人的销售单价至少是2050元.
答:![]() 型智能扫地机器人的销售单价至少是2050元.
型智能扫地机器人的销售单价至少是2050元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏思考解决如下问题:
原题:如图1,点
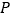 ,
,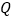 分别在菱形
分别在菱形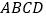 的边
的边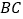 ,
,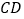 上,
上,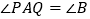 ,求证:
,求证: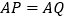 .
.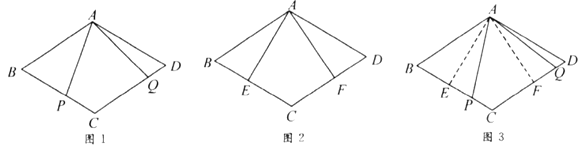
(1)小敏进行探索,若将点
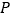 ,
,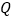 的位置特殊化:把
的位置特殊化:把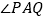 绕点
绕点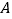 旋转得到
旋转得到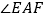 ,使
,使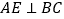 ,点
,点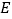 ,
,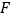 分别在边
分别在边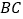 ,
,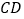 上,如图2,此时她证明了
上,如图2,此时她证明了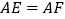 .请你证明.
.请你证明.(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作
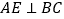 ,
,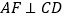 ,垂足分别为
,垂足分别为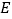 ,
,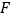 .请你继续完成原题的证明.
.请你继续完成原题的证明.(3)如果在原题中添加条件:
 ,
,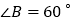 ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,3),B(5,1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
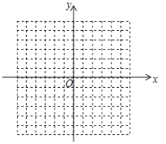
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于x轴对称的△A′B′C′,并写出△A′B′C′各顶点坐标;
(3)在x轴上找一点P,使PA+PB的值最小。请画出点P,并求出点P坐标。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 平面直角坐标系的原点,三角形
平面直角坐标系的原点,三角形 中,
中, ,顶点
,顶点 的坐标分别为
的坐标分别为 ,且
,且 .
.
(1)求三角形
 的面积;
的面积;(2)动点
 从点
从点 出发沿射线
出发沿射线 方向以每秒
方向以每秒 个单位长度的速度运动,设点
个单位长度的速度运动,设点 的运动时间为t秒.连接
的运动时间为t秒.连接 ,请用含t的式子表示三角形
,请用含t的式子表示三角形 的面积;
的面积;(3)在(2)的条件下,当三角形
 的面积为
的面积为 时,直线
时,直线 与
与 轴相交于点
轴相交于点 ,求点
,求点 的坐标
的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公交车行驶在笔直的公路上,这条路上有
 ,
,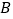 ,
,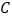 ,
,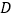 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从 站开往
站开往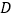 站的车称为上行车,从
站的车称为上行车,从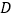 站开往
站开往 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从 站、
站、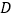 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 ,
,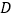 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)问第一班上行车到
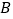 站、第一班下行车到
站、第一班下行车到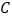 站分别用时多少?
站分别用时多少?(2)若第一班上行车行驶时间为
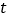 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为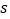 千米,求
千米,求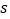 与
与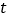 的函数关系式.
的函数关系式.(3)一乘客前往
 站办事,他在
站办事,他在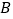 ,
,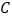 两站间的
两站间的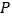 处(不含
处(不含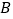 ,
,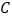 站),刚好遇到上行车,
站),刚好遇到上行车,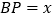 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到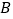 站或走到
站或走到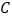 站乘下行车前往
站乘下行车前往 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求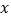 满足的条件.
满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.
 ∶
∶ C.
C. ∶
∶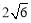 D.
D.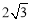 ∶
∶
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
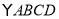 中,
中,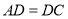 ,
,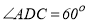 ,对角线
,对角线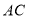 ,
,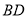 相交于点
相交于点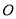 .点
.点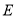 是线段
是线段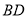 上一动点(不与
上一动点(不与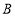 、
、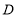 重合),连接
重合),连接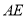 ,以
,以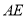 为边在
为边在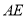 的右侧作
的右侧作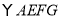 ,且
,且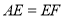 ,
,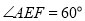 .
.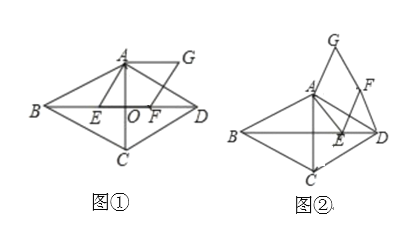
(1)如图①,若点
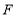 落在线段
落在线段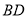 上,则线段
上,则线段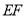 与线段
与线段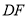 的数量关系是______;
的数量关系是______;(2)如图②,若点
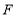 不在线段
不在线段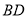 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
相关试题

