【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
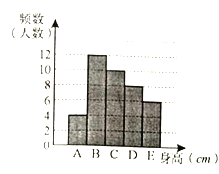
男生身高情况直方图
女生身高情况扇形统计图
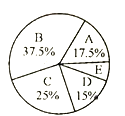
根据图表提供的信息,回答下列问题:
(1)求样本中男生的人数.
(2)求样本中女生身高在E组的人数.
(3)已知该校共有男生380人,女生320人,请估计全校身高在![]() 之间的学生总人数.
之间的学生总人数.
参考答案:
【答案】(1)40人;(2)2人;(3)全校身高在![]() 之间的学生有299人
之间的学生有299人
【解析】
(1)根据直方图直接将每组的人数相加即可;
(2)由(1)可得样本女生人数,求得E组所占百分比,然后即可求得E组人数;
(3)分别求得男生与女生D,E组所占百分比,然后用总人数求得答案即可.
解:(1)![]() (人)
(人)
![]() 样本中男生的人数是40人;
样本中男生的人数是40人;
(2)![]() (人),
(人),
![]() 样本中女生身高在E组的有2人;
样本中女生身高在E组的有2人;
(3)![]() (人),
(人),
![]() 全校身高在
全校身高在![]() 之间的学生有299人.
之间的学生有299人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的三个内角分别是
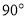 ,
,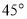 ,
,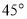 和
和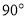 ,
,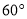 ,
,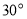 ,按如图所示叠放在一起(点
,按如图所示叠放在一起(点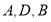 在同一直线上),若固定
在同一直线上),若固定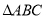 ,将
,将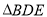 绕着公共顶点
绕着公共顶点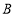 顺时针旋转
顺时针旋转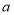 度(
度(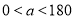 ),当边
),当边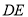 与
与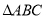 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角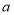 的值为_______.
的值为_______.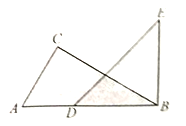
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一张平行四边形纸片ABCD(AB<BC),要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( )

A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)


图1 图2
(1)若该厂仓库里有1000张正方形纸板和2000张长方形纸板。问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?
(2)该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
相关试题

