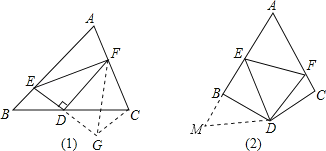
【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
参考答案:
【答案】(1)①见解析;②BE2+CF2=EF2.证明见解析;(2)EF= EB+CF,证明见解析.
【解析】
试题分析:(1)①如图(1)延长ED到G,使DG=ED,连接CG,FG,根据条件证明△DCG≌△DBE,得DG=DE,CG=BE,易证FD垂直平分线段EG,则FG=FE,把问题转化到△CFG中,运用三边关系比较大小;
②结论:BE2+CF2=EF2.若∠A=90°,则∠B+∠C=90°,可证∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,在Rt△CFG中,由勾股定理探索线段BE、CF、EF之间的数量关系;
(2)如图(2),结论:EF=EB+FC.延长AB到M,使BM=CF,根据条件证明△BDM≌△CDF,则DM=DF,再证明△DEM≌△DEF,从而得EF=EM=EB+BM=EB+CF.
(1)①证明:如图(1)延长ED到G,使DG=ED,连接CG,FG,
∵在△DCG与△DBE中,
 ,
,
∴△DCG≌△DBE(SAS),
∴DG=DE,CG=BE,
又∵DE⊥DF,
∴FD垂直平分线段EG,
∴FG=FE,
在△CFG中,CG+CF>FG,即BE+CF>EF;
②结论:BE2+CF2=EF2.
理由:∵∠A=90°,
∴∠B+∠ACD=90°,
由①∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,
即BE2+CF2=EF2;
(2)如图(2),结论:EF=EB+FC.
理由:延长AB到M,使BM=CF,
∵∠ABD+∠C=180°,又∠ABD+∠MBD=180°,
∴∠MBD=∠C,而BD=CD,
∴△BDM≌△CDF,
∴DM=DF,∠BDM=∠CDF,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠CDB﹣∠EDF=120°﹣60°=60°=∠EDF,
∴△DEM≌△DEF,
∴EF=EM=EB+BM=EB+CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
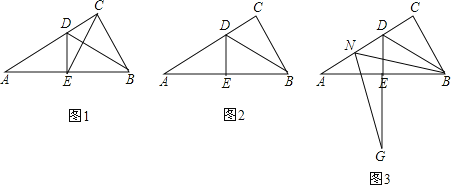
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区2012年屋顶绿化面积为2000平方米,计划2014年屋顶绿化面积要达到2880平方米,如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是3cm和7cm,它的周长是____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
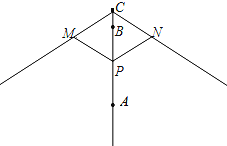
A.四边形PNCM可能会出现为正方形
B.四边形PNCM的周长始终不变
C.当∠CPN=60°时,CP=AP
D.四边形PNCM的面积始终不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=2,计算:a2b+ab2等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列命题,其中是真命题的是( )
A. 若甲对,则乙对 B. 若乙对,则甲对
C. 若乙错,则甲错 D. 若甲错,则乙对
相关试题

