【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)、根据题意画出树状图,根据树状图进行解答概率;(2)、根据树状图得出概率.
试题解析:(1)、画树状图得
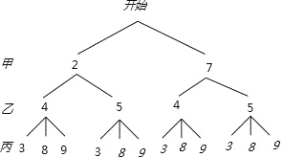
∴一共有12种等可能的结果,取出的3个小球的标号全是奇数的有2种情况,
∴取出的3个小球的标号全是奇数的概率是:P(全是奇数)= ![]() =
=![]()
(2)、∵这些线段能构成三角形的有2、4、3,7、4、8,7、4、9,7、5、3,7、5、8,7、5、9共6种情况,
∴这些线段能构成三角形的概率为P(能构成三角形)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别
身高
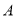
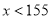
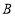
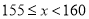
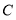
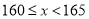
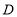
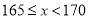
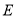
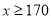
男生身高情况直方图
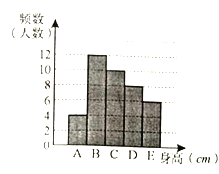
女生身高情况扇形统计图
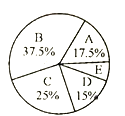
根据图表提供的信息,回答下列问题:
(1)求样本中男生的人数.
(2)求样本中女生身高在E组的人数.
(3)已知该校共有男生380人,女生320人,请估计全校身高在
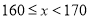 之间的学生总人数.
之间的学生总人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)


图1 图2
(1)若该厂仓库里有1000张正方形纸板和2000张长方形纸板。问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?
(2)该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
对于多项式
 ,如果我们把
,如果我们把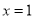 代入此多项式,发现
代入此多项式,发现 的值为0,这时可以确定多项式中有因式
的值为0,这时可以确定多项式中有因式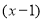 :同理,可以确定多项式中有另一个因式
:同理,可以确定多项式中有另一个因式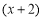 ,于是我们可以得到:
,于是我们可以得到: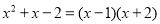 .
.又如:对于多项式
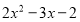 ,发现当
,发现当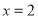 时,
时,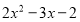 的值为0,则多项式
的值为0,则多项式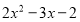 有一个因式
有一个因式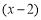 ,我们可以设
,我们可以设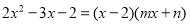 ,解得
,解得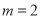 ,
,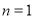 ,于是我们可以得到:
,于是我们可以得到: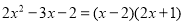 .
.请你根据以上材料,解答以下问题:
(1)当
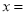 时,多项式
时,多项式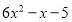 的值为0,所以多项式
的值为0,所以多项式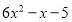 有因式 ,从而因式分解
有因式 ,从而因式分解 .
.(2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式.请你尝试用试根法分解多项式:①
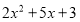 ;②
;②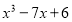 .
.(3)小聪用试根法成功解决了以上多项式的因式分解,于是他猜想:
代数式
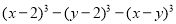 有因式 , , ,
有因式 , , ,所以分解因式
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
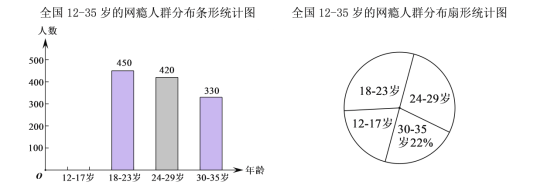
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁网瘾人数约为3600万,请估计其中12﹣23岁的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
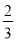 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.2万元,乙队每天的施工费用为5.8万元.工程预算的施工费用为501万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
相关试题

