【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.
![]()
(1)问运动多少秒时BC=2(单位长度)?
(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
参考答案:
【答案】(1)1或2;(2)1.5秒;(3)5或 3.5.
【解析】整体分析:
(1)分点B在点C的左边和点B在点C的右边两种情况讨论;(2)所走路程为这两条线段的和,用路程,速度,时间之间的关系可求解;(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.
解:(1)设运动t秒时,BC=2单位长度,
①当点B在点C的左边时,
由题意得:3t+2+t=6,
解得:t=1;
②当点B在点C的右边时,
由题意得:3t﹣2+t=6,
解得:t=2.
(2)(2+4)÷(3+1)=1.5(秒).
答:线段AB与线段CD从开始相遇到完全离开共经过1.5秒长时间.
(3)存在关系式BD﹣AP=3PC.
设运动时间为t秒,
①当t=(4+2)÷(3+1)=1.5时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD=4,
PA+3PC=AB+2PC=2+2PC,
当PC=1时,BD=AP+3PC,即BD﹣AP=3PC;
②当1.5<t<2.5时,点C在点A和点B之间,0<PC<2:
当点P在线段BC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+4PC=AB﹣BC+4PC=2﹣BC+4PC
当PC=0.5时,有BD=AP+3PC,即 BD﹣AP=3PC,
③当t=2.5时,点A与点C重合,0<PC≤2,BD=CD﹣AB=2,AP+3PC=4PC,
当PC=0.5时,有BD=AP+3PC,即BD﹣AP=3PC,
∵P在C点左侧或右侧,
∴PD的长有2种可能,即5或3.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份
中心城区人口数
中心城区人均住房建筑面积(单位:平方米)
中心城区住房建筑面积(单位:万平凡米)
2013年
180
30
5400
2014年
2015年
(2)求题目中的a和m.
-
科目: 来源: 题型:
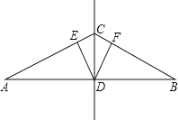
查看答案和解析>>【题目】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);
(2)与y=
 x2的开口大小相同,方向相反;
x2的开口大小相同,方向相反;(3)当x的值由0增加到2时,函数值减少4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一个直角坐标系中作出y=
 x2,y=
x2,y= x2-1的图象.
x2-1的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=
 x2-1与抛物线y=
x2-1与抛物线y= x2有什么关系?
x2有什么关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】健身运动已成为时尚,某公司计划组装
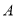 、
、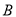 两种型号的健身器材共
两种型号的健身器材共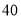 套,捐给社区健身中心。组装一套
套,捐给社区健身中心。组装一套 型健身器材需甲种部件
型健身器材需甲种部件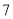 个和乙种部件
个和乙种部件 个,组装一套
个,组装一套 型健身器材需甲种部件
型健身器材需甲种部件 个和乙种部件
个和乙种部件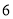 个.公司现有甲种部件
个.公司现有甲种部件 个,乙种部件
个,乙种部件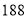 个.
个.(
 )公司在组装
)公司在组装 、
、 两种型号的健身器材时,共有多少种组装方案?
两种型号的健身器材时,共有多少种组装方案?(
 )组装一套
)组装一套 型健身器材需费用
型健身器材需费用 元,组装一套
元,组装一套 型健身器材需费用
型健身器材需费用 元,求总组装费用最少的组装方案,并求出最少组装费用?
元,求总组装费用最少的组装方案,并求出最少组装费用?
相关试题

