【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

参考答案:
【答案】见解析
【解析】试题分析:(1)、根据AB=AC可得∠B=∠C,根据DE⊥AB,DF⊥AC可得∠BED=∠CFD=90°,根据D为中点可得BD=CD,根据AAS可以判定三角形全等;(2)、根据三个角为直角的四边形是矩形,首先得出矩形,然后根据(1)的结论说明有一组邻边相等.
试题解析:(1)、∵AB=AC ∴∠B=∠C ∵DE⊥AB,DF⊥AC ∴∠BED=∠CFD=90°
∵D为BC的中点 ∴BD=CD ∴△BED≌△CFD
(2)、∵DE⊥AB,DF⊥AC ∴∠AED=∠AFD=90° 又∵∠A=90°
∴四边形DFAE为矩形 ∵△BED≌△CFD ∴DE=DF ∴四边形DFAE为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);
(2)与y=
 x2的开口大小相同,方向相反;
x2的开口大小相同,方向相反;(3)当x的值由0增加到2时,函数值减少4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.

(1)问运动多少秒时BC=2(单位长度)?
(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一个直角坐标系中作出y=
 x2,y=
x2,y= x2-1的图象.
x2-1的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=
 x2-1与抛物线y=
x2-1与抛物线y= x2有什么关系?
x2有什么关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】健身运动已成为时尚,某公司计划组装
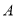 、
、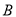 两种型号的健身器材共
两种型号的健身器材共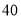 套,捐给社区健身中心。组装一套
套,捐给社区健身中心。组装一套 型健身器材需甲种部件
型健身器材需甲种部件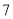 个和乙种部件
个和乙种部件 个,组装一套
个,组装一套 型健身器材需甲种部件
型健身器材需甲种部件 个和乙种部件
个和乙种部件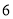 个.公司现有甲种部件
个.公司现有甲种部件 个,乙种部件
个,乙种部件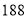 个.
个.(
 )公司在组装
)公司在组装 、
、 两种型号的健身器材时,共有多少种组装方案?
两种型号的健身器材时,共有多少种组装方案?(
 )组装一套
)组装一套 型健身器材需费用
型健身器材需费用 元,组装一套
元,组装一套 型健身器材需费用
型健身器材需费用 元,求总组装费用最少的组装方案,并求出最少组装费用?
元,求总组装费用最少的组装方案,并求出最少组装费用? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥形和烟囱帽的底面直径是40cm,母线长是120cm,需要加工这样的一个烟囱帽,请你画一画:
(1)至少需要多少厘米铁皮(不计接头)
(2)如果用一张圆形铁皮作为材料来制作这个烟囱帽,那么这个圆形铁皮的半径至少应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

相关试题

