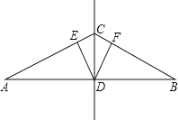
【题目】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)CD=![]() AB时,四边形CEDF为正方形,理由见解析.
AB时,四边形CEDF为正方形,理由见解析.
【解析】
试题分析:(1)由CD垂直平分线AB,可得AC=CB,∴∠ACD=∠BCD,再加∠EDC=∠FDC=90°,可证得△ACD≌△BCD(ASA),∴CE=CF;
(2)因为有三个角是直角,且邻边相等的四边形是正方形.所以当CD=![]() AB时,四边形CEDF为正方形.
AB时,四边形CEDF为正方形.
(1)证明:∵CD垂直平分线AB,
∴AC=CB.
∴△ABC是等腰三角形,
∵CD⊥AB,
∴∠ACD=∠BCD.
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°
∴∠EDC=∠FDC,
在△DEC与△DFC中,
 ,
,
∴△DEC≌△DFC(ASA),
∴CE=CF.
(2)解:当CD=![]() AB时,四边形CEDF为正方形.理由如下:
AB时,四边形CEDF为正方形.理由如下:
∵CD⊥AB,
∴∠CDB=∠CDA=90°,
∵CD=![]() AB,
AB,
∴CD=BD=AD,
∴∠B=∠DCB=∠ACD=45°,
∴∠ACB=90°,
∴四边形ECFD是矩形,
∵CE=CF,
∴四边形ECFD是正方形.
考点: 1.线段垂直平分线的性质;2.正方形的判定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
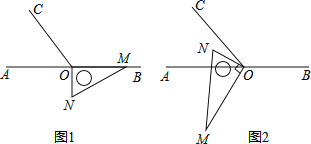
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份
中心城区人口数
中心城区人均住房建筑面积(单位:平方米)
中心城区住房建筑面积(单位:万平凡米)
2013年
180
30
5400
2014年
2015年
(2)求题目中的a和m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);
(2)与y=
 x2的开口大小相同,方向相反;
x2的开口大小相同,方向相反;(3)当x的值由0增加到2时,函数值减少4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.

(1)问运动多少秒时BC=2(单位长度)?
(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一个直角坐标系中作出y=
 x2,y=
x2,y= x2-1的图象.
x2-1的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=
 x2-1与抛物线y=
x2-1与抛物线y= x2有什么关系?
x2有什么关系?
相关试题

