【题目】如图,甲、乙两人分别从A(1, ![]() )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 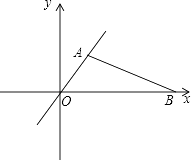
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
参考答案:
【答案】
(1)证明:因为A坐标为(1, ![]() ),
),
所以OA=2,∠AOB=60°.
因为OM=2﹣4t,ON=6﹣4t,
当 ![]() =
= ![]() 时,解得t=0,
时,解得t=0,
即在甲、乙两人到达O点前,只有当t=0时,△OMN∽△OAB,所以MN与AB不可能平行
(2)证明:因为甲达到O点时间为t= ![]() ,乙达到O点的时间为t=
,乙达到O点的时间为t= ![]() =
= ![]() ,所以甲先到达O点,所以t=
,所以甲先到达O点,所以t= ![]() 或t=
或t= ![]() 时,O、M、N三点不能连接成三角形,
时,O、M、N三点不能连接成三角形,
①当t< ![]() 时,如果△OMN∽△OBA,则有
时,如果△OMN∽△OBA,则有 ![]() =
= ![]() ,解得t=2>
,解得t=2> ![]() ,所以,△OMN不可能相似△OBA;
,所以,△OMN不可能相似△OBA;
②当 ![]() <t<
<t< ![]() 时,∠MON>∠AOB,显然△OMN不相似△OBA;
时,∠MON>∠AOB,显然△OMN不相似△OBA;
③当t> ![]() 时,
时, ![]() =
= ![]() ,解得t=2>
,解得t=2> ![]() ,所以当t=2时,△OMN∽△OBA
,所以当t=2时,△OMN∽△OBA
(3)证明:①当t≤ ![]() 时,如图1,过点M作MH⊥x轴,垂足为H,
时,如图1,过点M作MH⊥x轴,垂足为H,
在Rt△MOH中,因为∠AOB=60°,
所以MH=OMsin60°=(2﹣4t)× ![]() =
= ![]() (1﹣2t),
(1﹣2t),
OH=0Mcos60°=(2﹣4t)× ![]() =1﹣2t,
=1﹣2t,
所以NH=(6﹣4t)﹣(1﹣2t)=5﹣2t,
所以s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
②当 ![]() <t≤
<t≤ ![]() 时,如图2,作MH⊥x轴,垂足为H,
时,如图2,作MH⊥x轴,垂足为H,
在Rt△MOH中,MH= ![]() (4t﹣2)=
(4t﹣2)= ![]() (2t﹣1),NH=
(2t﹣1),NH= ![]() (4t﹣2)+(6﹣4t)=5﹣2t,
(4t﹣2)+(6﹣4t)=5﹣2t,
所以s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
③当t> ![]() 时,同理可得s=[
时,同理可得s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28,
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28,
综上所述,s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28.
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28.
因为s=16t2﹣32t+28=16(t﹣1)2+12,
所以当t=1时,s有最小值为12,所以甲、乙两人距离最小值为2 ![]() km.
km.


【解析】(1)用反证法说明.根据已知条件分别表示相关线段的长度,根据三角形相似得比例式说明;(2)根据两个点到达O点的时间不同分段讨论解答;(3)在不同的时间段运用相似三角形的判定和性质分别求解析式,运用函数性质解答问题.
【考点精析】利用二次函数的最值和勾股定理的概念对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,
 ≈1.41,
≈1.41,  ≈2.24)
≈2.24)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.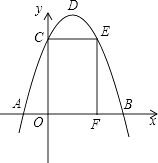
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4x+7=12x﹣5 (2)4y﹣3(5﹣y)=6;
(3)
 (4)
(4) =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,
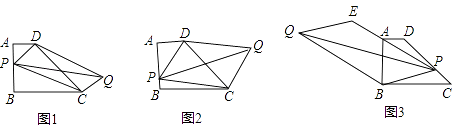
问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差km/h.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)22﹣20120+(﹣6)÷3;
(2) .
.
相关试题

