搜索
【题目】如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差km/h． 
参考答案：
【答案】4
【解析】解：根据图象可得： ∵甲行驶距离为100千米时，行驶时间为5小时，乙行驶距离为80千米时，行驶时间为5小时，
∴甲的速度是：100÷5=20（千米/时）；乙的速度是：80÷5=16（千米/时）；
故这两人骑自行车的速度相差：20﹣16=4（千米/时）；
解法二：利用待定系数法s=k甲t+b，s=k乙t，
易得得k甲=16，k乙=20，
∵速度=路程÷时间
所以k甲、k乙分别为甲、乙的速度
故速度差为20﹣16=4km/h
故答案为：4．
根据图中信息找出甲，乙两人行驶的路程和时间，进而求出速度即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程：
（1）4x+7＝12x﹣5 （2）4y﹣3（5﹣y）＝6；
（3）
（4）
＝1． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，甲、乙两人分别从A（1，
）、B（6，0）两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．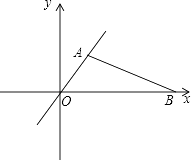 
（1）请说明甲、乙两人到达O点前，MN与AB不可能平行；
（2）当t为何值时，△OMN∽△OBA；
（3）甲、乙两人之间的距离为MN的长，设s=MN2 ， 求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，
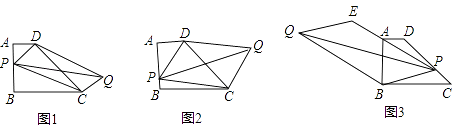
问题1：如图1，P为AB边上的一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？
问题2：如图2，若P为AB边上一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
问题3：若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE=nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）22﹣20120+（﹣6）÷3；
（2）
． -
科目： 来源： 题型：
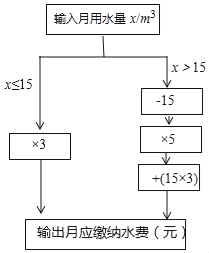
查看答案和解析>>【题目】小明根据市自来水公司的居民用水收费标准，制定了水费计算数值转换机的示意图．（用水量单位：m3，水费单位：元）
（1）根据转换机程序计算下列各户月应缴纳水费
用户
张大爷
王阿姨
小明家
月用水量/m3
6
15
17
月应缴纳水费/元
（2）当x＞15时，用含x的代数式表示水费 ；
（3）小丽家10月份水费是70元，小丽家10月份用水 m3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程:
(1)4-
m=-m; (2)56-8x=11+x;(3)
x+1=5+
x; (4)-5x+6+7x=1+2x-3+8x.
相关试题
