【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3, 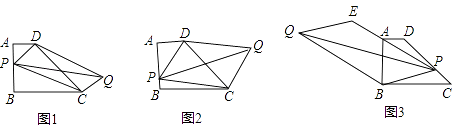
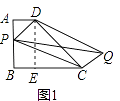
问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
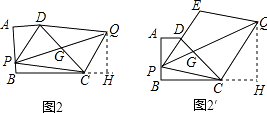
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
参考答案:
【答案】解:问题1:过点D作DE⊥BC于点E, ∵梯形ABCD,AD∥BC,AB⊥BC
∴四边形ABED是矩形,
∴DE=AB=2,BE=AD=1,
∴CE=BC﹣BE=2,
∴DC=2 ![]() ,
,
∵四边形PCQD是平行四边形,
若对角线PQ、DC相等,则四边形PCQD是矩形,
设PB=x,则AP=2﹣x,
在Rt△DPC中,PD2+PC2=DC2 , 即x2+32+(2﹣x)2+1=8,
化简得x2﹣2x+3=0,
∵△=(﹣2)2﹣4×1×3=﹣8<0,
∴方程无解,
∴对角线PQ与DC不可能相等.
问题2:如图2,在平行四边形PCQD中,设对角线PQ与DC相交于点G,
则G是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
∴Rt△ADP≌Rt△HCQ,
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
问题3:如图2′,设PQ与DC相交于点G,
∵PE∥CQ,PD=DE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴G是DC上一定点,
作QH⊥BC,交BC的延长线于H,
同理可证∠ADP=∠QCH,
∴Rt△ADP∽Rt△HCQ,
即 ![]() =
= ![]() =
= ![]() ,
,
∴CH=2,
∴BH=BC+CH=3+2=5,
∴当PQ⊥AB时,PQ的长最小,即为5.
问题4:如图3,设PQ与AB相交于点G,连接DG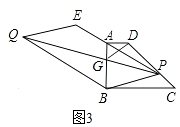
∵PE∥BQ,AE=nPA,
∴ ![]() =
= ![]() ,
,
∴G是AB上一定点,
∵四边形PBQE是平行四边形,
∴ ![]() =
= ![]() =
= ![]()
∴当GP最小时,QP有最小值
在△GDP中,当GP⊥CD时,GP最小,
当PQ垂直于CD时,P点在CD的延迟线上,
∴当点P与点D重合时,GP取最小值,
∴QPmin=QD
∵AB=2
∴AG= ![]() ,
,
∴DG= 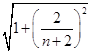 =
= ![]() ,
,
∴QD= ![]() DG=
DG= ![]()
![]() =
= ![]() ,
,
∴QPmin=QD= 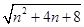 ,
,
故对角线PQ的最小值为 ![]() .
.
【解析】问题1:四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,然后利用矩形的性质,设PB=x,可得方程x2+32+(2﹣x)2+1=8,由判别式△<0,可知此方程无实数根,即对角线PQ,DC的长不可能相等; 问题2:在平行四边形PCQD中,设对角线PQ与DC相交于点G,可得G是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB时,PQ的长最小,即为4;
问题3:设PQ与DC相交于点G,PE∥CQ,PD=DE,可得 ![]() =
= ![]() =
= ![]() ,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案;
,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案;
问题4:设PQ与AB相交于点G,连接DG,由平行四边形PBQE得 ![]() =
= ![]() ,可知G为定点,由△GDP性质可知点D、P重合时GP最小,即GP最小为DP.
,可知G为定点,由△GDP性质可知点D、P重合时GP最小,即GP最小为DP.
【考点精析】本题主要考查了求根公式和勾股定理的概念的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.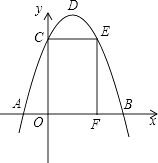
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4x+7=12x﹣5 (2)4y﹣3(5﹣y)=6;
(3)
 (4)
(4) =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人分别从A(1,
 )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差km/h.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)22﹣20120+(﹣6)÷3;
(2) .
. -
科目: 来源: 题型:
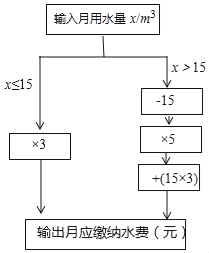
查看答案和解析>>【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户
张大爷
王阿姨
小明家
月用水量/m3
6
15
17
月应缴纳水费/元
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
相关试题

