搜索
【题目】解下列方程：
（1）4x+7＝12x﹣5 （2）4y﹣3（5﹣y）＝6；
（3）
（4）
＝1．
参考答案：
【答案】(1) x＝
；(2) y＝3；（3）x＝﹣1；（4）a＝4.4．
【解析】
(1)(2)移项再合并同类项即可解答.
(3)(4)先去分母，去括号，再移项合并同类项即可解答.
解：（1）移项，得：4x﹣12x＝﹣5﹣7，
合并同类项，得：﹣8x＝﹣12，
系数化为1，得：x＝
；
（2）去括号，得：4y﹣15+3y＝6，
移项，得：4y+3y＝6+15，
合并同类项，得：7y＝21，
系数化为1，得：y＝3；
（3）去分母，得：3（3x﹣1）﹣2（5x﹣7）＝12，
去括号，得：9x﹣3﹣10x+14＝12，
移项，得：9x﹣10x＝12+3﹣14，
合并同类项，得：﹣x＝1，
系数化为1，得：x＝﹣1；
（4）整理，得：
﹣
＝1，
去分母，得：3（20a﹣3）﹣5（10a+4）＝15，
去括号，得：60a﹣9﹣50a﹣20＝15，
移项，得：60a﹣50a＝15+9+20，
合并同类项，得：10a＝44，
系数化为1，得：a＝4.4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的圆心在坐标原点，半径为2，直线y=x+b（b＞0）与⊙O交于A、B两点，点O关于直线y=x+b的对称点O′．
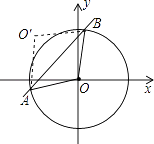
（1）求证：四边形OAO′B是菱形；
（2）当点O′落在⊙O上时，求b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知B港口位于A观测点北偏东53.2°方向，且其到A观测点正北方向的距离BD的长为16km，一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行，15min后达到C处，现测得C处位于A观测点北偏东79.8°方向，求此时货轮与A观测点之间的距离AC的长（精确到0.1km）．（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin79.8°≈0.98，cos79.8°≈0.18，tan26.6°≈0.50，
≈1.41， 
≈2.24）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3，
（1）求抛物线所对应的函数解析式；
（2）求△ABD的面积；
（3）将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．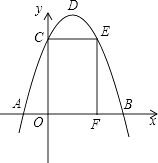
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，甲、乙两人分别从A（1，
）、B（6，0）两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．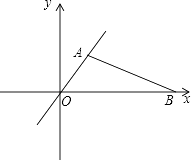 
（1）请说明甲、乙两人到达O点前，MN与AB不可能平行；
（2）当t为何值时，△OMN∽△OBA；
（3）甲、乙两人之间的距离为MN的长，设s=MN2 ， 求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，
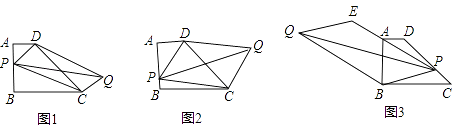
问题1：如图1，P为AB边上的一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？
问题2：如图2，若P为AB边上一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
问题3：若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE=nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差km/h．
相关试题
