搜索
【题目】如图，在一个18米高的楼顶上有一信号塔DC，李明同学为了测量信号塔的高度，在地面的A处测的信号塔下端D的仰角为30°，然后他正对塔的方向前进了18米到达地面的B处，又测得信号塔顶端C的仰角为60°，CD⊥AB与点E，E、B、A在一条直线上．请你帮李明同学计算出信号塔CD的高度（结果保留整数，
≈1.7，
≈1.4 ）.
参考答案：
【答案】解：根据题意得：AB=18，DE=18，∠A=30°，∠EBC=60°，
在Rt△ADE中，AE=
=
=18
,
∴BE=AE﹣AB=18﹣18，
在Rt△BCE中，CE=BEtan60°=（18﹣18）=54﹣18，
∴CD=CE﹣DE=54﹣18﹣18≈5米.
【解析】利用30°的正切值即可求得AE长，进而可求得CE长．CE减去DE长即为信号塔CD的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：|﹣
|﹣（
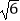﹣π）0﹣sin30°+（﹣）﹣2 -
科目： 来源： 题型：
查看答案和解析>>【题目】规定两数a、b之间的一种运算，记作（a，b）：如果
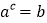，那么（a，b）=c．例如：因为
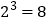，所以（2，8）=3.（1）根据上述规定，填空：
（5，125）= ，（-2，4）= ，（-2，-8）= ；
（2）小明在研究这种运算时发现一个现象：
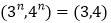，他给出了如下的证明：设
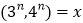，则
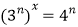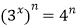
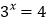，即
∴
，即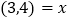
，∴
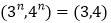．请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4，5)＋(4，6)=(4，30)
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，在正方形ABCD中，E、F分别是边BC、CD上的点，且∠EAF=45°，把△ADF绕着点A顺时针旋转90°得到△ABG，请直接写出图中所有的全等三角形；
（2）在四边形ABCD中，AB=AD，∠B=∠D=90°.
①如图2，若E、F分别是边BC、CD上的点，且2∠EAF=∠BAD，求证：EF=BE+DF；
②若E、F分别是边BC、CD延长线上的点，且2∠EAF=∠BAD，①中的结论是否仍然成立？请说明理由
-
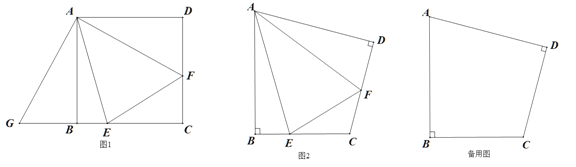
科目： 来源： 题型：
查看答案和解析>>【题目】中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了 名学生.
（2）将图1、图2补充完整；
（3）现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB.
（1）求证：PB是的切线；
（2）若PB=6，DB=8，求⊙O的半径 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=﹣2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．
相关试题
