【题目】如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为;用含t的式子表示点P的坐标为;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?
(3)试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ![]() ?若存在,求出点T的坐标;若不存在,请说明理由.
?若存在,求出点T的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)(6,4);(t, ![]() t)
t)
(2)
解:∵S△OMP= ![]() ×OM×
×OM× ![]() t,
t,
∴S= ![]() ×(6﹣t)×
×(6﹣t)× ![]() t=﹣
t=﹣ ![]() t2+2t=﹣
t2+2t=﹣ ![]() (t﹣3)2+3(0<t<6).
(t﹣3)2+3(0<t<6).
∴当t=3时,S有最大值.
(3)
解:存在.理由如下:
由(2)得,当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:y= ![]() x.
x.
设点T的坐标为(0,b),则直线MT的函数关系式为:y=﹣ ![]() x+b,
x+b,
解方程组 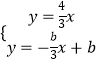 得
得 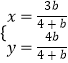 ,
,
∴直线ON与MT的交点R的坐标为( ![]() ,
, ![]() ),
),
∵S△OCN= ![]() ×4×3=6,
×4×3=6,
∴S△ORT= ![]() S△OCN=2,
S△OCN=2,
①当点T在点O、C之间时,分割出的三角形是△OR1T1,
如图2所示,作R1D1⊥y轴,D1为垂足,则S△OR1T1= ![]() RD1OT=
RD1OT= ![]()
![]() b=2.
b=2.
∴3b2﹣4b﹣16=0,
解得:b= ![]() (负值舍去).
(负值舍去).
∴b= ![]() ,
,
此时点T1的坐标为(0, ![]() ).
).
②当点T在OC的延长线上时,分割出的三角形是△R2NE,如图,设MT交CN于点E,
由①得点E的横坐标为 ![]() ,作R2D2⊥CN交CN于点D2,则
,作R2D2⊥CN交CN于点D2,则
S△R2NE= ![]() ENR2D2=
ENR2D2= ![]() (3﹣
(3﹣ ![]() )(4﹣
)(4﹣ ![]() =
= ![]() =2.
=2.
∴b2+4b﹣48=0,
解得:b=±2 ![]() ﹣2(负值舍去).
﹣2(负值舍去).
∴b=2 ![]() ﹣2.
﹣2.
∴此时点T2的坐标为(0,2 ![]() ).
).
综上所述,在y轴上存在点T1(0, ![]() ),T2(0,2
),T2(0,2 ![]() ﹣2)符合条件.
﹣2)符合条件.
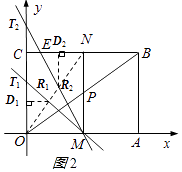
【解析】解:(1)延长NP交OA于H,如图1所示:
∵矩形OABC,
∴BC∥OA,∠OCB=90°,
∵PN⊥BC,
∴NH∥OC,
∴四边形CNHO是平行四边形,
∴OH=CN,
∵OA=6,AB=4,
∴点B的坐标为(6,4);
由图可得,点P的横坐标=0H=CN=t,纵坐标=4﹣NP,
∵NP⊥BC,
∴NP∥OC,
∴NP:OC=BN:CB,
即NP:4=(6﹣t):6,
∴NP=4﹣ ![]() t,
t,
∴点P的纵坐标=4﹣NP= ![]() t,
t,
则点P的坐标为(t, ![]() t);
t);
所以答案是:(6,4);(t, ![]() t);
t);
【考点精析】根据题目的已知条件,利用二次函数的最值和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b的图象与反比例函数y2=
 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=  的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当y1<y2<0时,写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.

(1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案. Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
(1)求出y1、y2与工龄x之间的函数关系式;
(2)现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?
(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )

A.3
B.3
C.3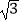
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.“蒙上眼睛射击正中靶心”是必然事件
B.“抛一枚硬币,正面朝上的概率为 ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在  附近
附近
D.为了解某种节能灯的使用寿命,应选择全面调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图: ①分别以B、C为圆心,以大于
 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
A.50°
B.45°
C.30°
D.25°
相关试题

