【题目】某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案. Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
(1)求出y1、y2与工龄x之间的函数关系式;
(2)现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?
(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?
参考答案:
【答案】
(1)解:设y1与x之间的函数关系式为y1=kx,
由题意,得100=10k,
解得:k=10
∴y1=10x(x≥0,x为整数);
当0≤x≤3时,y2与x之间的函数关系式为y2=k2x,
由题意,得60=3k2.
∴k2=20,
∴y2=20x,
当3<x≤32时,设y2=a(x﹣23)2+860,
由题意,得698=a(32﹣23)2+860,
解得:a=﹣2,
∴y2=﹣2(x﹣23)2+860,
当32<x≤42时,由图象,得y2=698.
∴y2=  ;
;
(2)解:小张在原厂的社会工龄为:18﹣18=0年,企业工龄为:28﹣28=10年
y1=0,y2=522,
∴在小张在原厂的工龄工资为:0+522=522元,
当小张回家乡到后进该企业,小张的社会工龄为:28﹣18=10年,企业工龄为:28﹣28=0年
∴小张的工龄工资为;y1+y2=10×10+20×0=100
∴小张的第一年工龄工资每月下降了:522﹣100=422元,
答:第一年每月工龄工资下降422元;
(3)解:依题知要李程师的总工龄为:48﹣18=30,设李工程师的工龄工资为y,在本企业工作x年,
由题意,得3<x≤30
∴y=y1+y2=10(30﹣x)+[﹣2(x﹣23)2+860]=﹣2(x﹣20.5)2+942.5,
∵a=﹣2<0,
∴抛物线开口向下,对称轴是x=20.5,
∵x为整数,
∴当x=20或21时,y最大,且最大值为942,
∴李工程师的工龄工资最高为942元/月.
【解析】(1)结合函数图象根据待定系数法就可以得出y1、y2与工龄x之间的函数关系式,注意y2与x的函数关系式需要分段讨论;(2)根据(1)的解析式分别求出小张在原厂的工龄工资和回乡后的工龄工资,求出其差就可以了;(3)设李工程师的工龄工资为y,在本企业工作x年,根据工龄工资=社会工龄工资+企业工龄工资求出y与x之间的关系式,由二次函数的性质就可以求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知边长为6的等边△ABC内接于⊙O.

(1)求⊙O半径;
(2)求 的长和弓形BC的面积.
的长和弓形BC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b的图象与反比例函数y2=
 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=  的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当y1<y2<0时,写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.

(1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.

(1)点B的坐标为;用含t的式子表示点P的坐标为;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?
(3)试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ?若存在,求出点T的坐标;若不存在,请说明理由.
?若存在,求出点T的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )

A.3
B.3
C.3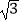
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.“蒙上眼睛射击正中靶心”是必然事件
B.“抛一枚硬币,正面朝上的概率为 ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在  附近
附近
D.为了解某种节能灯的使用寿命,应选择全面调查
相关试题

