【题目】阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如![]() 是方程
是方程![]() 的一个解,对应点
的一个解,对应点![]() ,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点
,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点![]() 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程
将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程![]() 的解.所以,我们就把条直线就叫做方程
的解.所以,我们就把条直线就叫做方程![]() 的图象.
的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知![]() 、
、![]() 、
、![]() ,则点__________(填“A或
,则点__________(填“A或![]() 或
或![]() ”)在方程
”)在方程![]() 的图象上.
的图象上.
(2)求方程![]() 和方程
和方程![]() 图象的交点坐标.
图象的交点坐标.
(3)已知以关于![]() 的方程组
的方程组![]() 的解为坐标的点在方程
的解为坐标的点在方程![]() 的图象上,当
的图象上,当![]() 时,化简
时,化简![]() .
.

参考答案:
【答案】(1)C;(2)(3,1);(3)![]()
【解析】
(1)利用图象法即可解决问题;
(2)求出方程组的解,即为两个方程的图象的交点坐标;
(3)解方程组求出m的值,根据绝对值的性质进行化简即可.
解:(1)如图,观察图象可知:点C在方程2xy=1的图象上,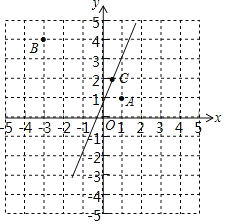
故答案为C.
(2)由![]() ,
,
解得![]() ,
,
∴方程2x+3y=9和方程3x4y=5图象的交点坐标为(3,1);
(3)由![]() ,解得
,解得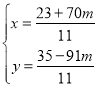 ,
,
∵x+y=5,
∴![]() +
+ ![]() =5,
=5,
∴m=![]() ,
,
当t>![]() 时,
时,![]() |17t|=t+2+17t=36t.
|17t|=t+2+17t=36t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数
 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )
A. ﹣2 B. ﹣4 C. ﹣
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A.B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=kx-1上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=kx-1上,则a的值是( )

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等边三角形,如图①,点D、E分别在射线BA、BC上,且AD=CE,求证:△BDE是等边三角形;

(2)如图②,点D在BA边上,点E在射线BC上,AD=CE,连接DE交AC于点F,请问DF与EF的数量关系是什么?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正方形
中,正方形 中心在原点,且顶点
中心在原点,且顶点 的坐标为
的坐标为 .动点
.动点 分别从点
分别从点 同时出发,绕着正方形的边按顺时针方向运动,当
同时出发,绕着正方形的边按顺时针方向运动,当 点回到
点回到 点时两点同时停止运动,运动时间为
点时两点同时停止运动,运动时间为 秒.连接
秒.连接 ,线段
,线段 、
、 与正方形的边围成的面积较小部分的图形记为
与正方形的边围成的面积较小部分的图形记为 .
.(1)请写出
 点的坐标.
点的坐标.(2)若
 的速度均为1个单位长度秒,试判断在运动过程中,
的速度均为1个单位长度秒,试判断在运动过程中, 的面积是否发生变化,如果不变求出该值,如果变化说明理由.
的面积是否发生变化,如果不变求出该值,如果变化说明理由.(3)若
 点速度为2个单位长度秒,
点速度为2个单位长度秒, 点为1个单位长度/秒,当
点为1个单位长度/秒,当 的面积为
的面积为 时,求
时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
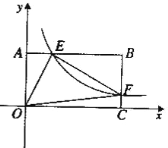
查看答案和解析>>【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数
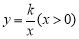 的图象与边BC交于点F。
的图象与边BC交于点F。【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求
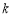 的值:
的值:【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
相关试题

