Question

【题目】已知，△ABC是等边三角形，如图①，点D、E分别在射线BA、BC上，且AD=CE，求证：△BDE是等边三角形；

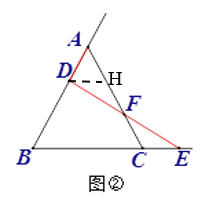
（2）如图②，点D在BA边上，点E在射线BC上，AD=CE，连接DE交AC于点F，请问DF与EF的数量关系是什么？并说明理由.

Answer 1

【答案】（1）见解析；（2）DF=EF，理由见解析.

【解析】

（1）利用有一个角是60度的等腰三角形是等边三角形进行判定；

（2）过点D作DH∥BE交AC于点H，证得△DHF≌△ECF（ASA），可得出DF=EF.

（1）证明：∵△ABC是等边三角形，

∴∠B =60°，AB=BC,

∵AD=CE,

∴AB+AD=BC+CE,即BD=BE,

∴△BDE是等腰三角形，

又∵∠B =60°，

∴△BDE是等边三角形；

（2）DF=EF，理由是：

如图②，过点D作DH∥BE交AC于点H，

∵△ABC是等边三角形，

∴∠A=∠B =∠ACB=60°，

∵DH∥BE，

∴∠ADH=∠B =60°，∠AHD=∠ACB =60°，

∴△ADH是等边三角形，

∴AD=DH,

∵AD=CE，

∴DH=CE,

∵DH∥BE，

∴∠HDF=∠E, ∠DHF=∠FCE,

在△DHF和△ECF中，

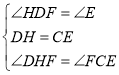
∴△DHF≌△ECF（ASA）

∴DF=EF