Question

【题目】如图1，四边形ABCD是正方形，AB=4，点G在BC边上，BG=3，DE⊥AG于点E，BF⊥AG于点F．

（1）求BF和DE的长；

（2）如图2，连接DF、CE，探究并证明线段DF与CE的数量关系与位置关系．

Answer 1

【答案】（1）；（2）DF=CE，DF⊥CE．理由见解析；

【解析】（1）如图1，先利用勾股定理计算出AG==5，再利用面积法和勾股定理计算出 然后证明△ABF≌△DAE，得到DE=AF=；
（2）作CH⊥DE于H，如图2，先利用△ABF≌△DAE,得到则与（1）的证明方法一样可得△CDH≌△DAE，则 于是可判断EH=EF，接着证明△DEF≌△CHE，所以DF=CE，∠EDF=∠HCE，然后利用三角形内角和得到从而判断DF⊥CE.

(1)如图1，

∵四边形ABCD是正方形，

∴，

∵DE⊥AG，BF⊥AG，

∴

在Rt△ABG中,AG==5，

∵

∴

∴AF===，

∵

∴∠ABF=∠DAE，

在△ABF和△DAE中

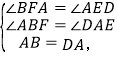
∴△ABF≌△DAE，

∴DE=AF=；

(2)DF=CE，DF⊥CE.理由如下：

作CH⊥DE于H，如图2，

∵△ABF≌△DAE,

∴

∴

与(1)的证明方法一样可得△CDH≌△DAE，

∴

∴

∴EH=EF，

在△DEF和△CHE中

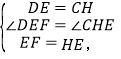
∴△DEF≌△CHE，

∴DF=CE，∠EDF=∠HCE，

∵∠1=∠2，

∴

∴DF⊥CE.