【题目】我县某商场计划购进甲、乙两种商品共80件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 | 15 | 20 |
乙种商品 | 25 | 35 |
设其中甲种商品购进x件,售完此两种商品总利润为y元.
(1)写出y与x的函数关系式.
(2)该商场计划最多投入1500元用于购进这两种商品共80件,则至少要购进多少件甲种商品?若售完这些商品,商场可获得的最大利润是多少元?
参考答案:
【答案】(1)y=-5x+800;(2)至少要购进50件甲种商品;售完这些商品,商场可获得的最大利润是550元.
【解析】(1)根据总利润=甲种商品利润+乙种商品利润即可解决问题.
(2)设购进甲种商品x件,列出不等式即可解决问题,然后根据一次函数的增减性解决最大值问题.
(1) 设购进甲种商品x件,则购进乙种商品(80-x)件,由题意,得
y=5x+10(80x)=5x+800.
(2)设购进甲种商品x件,由题意![]()
解得![]()
∴至少要购进50件甲种商品。
∵y=5x+800,
∴k=5<0,
∴y随x增大而减小,
∴x=50时,y最大值=550元.
∴售完这些商品,商场可获得的最大利润是550元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.
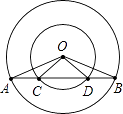
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
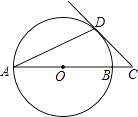
(1)求证:CD是⊙O的切线.
(2)若AB=2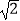 ,求OC的长.
,求OC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数
 的图象与正比例函数
的图象与正比例函数 的图象交于点A(m,4).
的图象交于点A(m,4).(1)求m、n的值;
(2)设一次函数
 的图象与x轴交于点B,求△AOB的面积;
的图象与x轴交于点B,求△AOB的面积;(3)直接写出使函数
 的值小于函数
的值小于函数 的值的自变量x的取值范围.
的值的自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点.

(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


相关试题

