【题目】已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
参考答案:
【答案】
(1)
解:∵a=1>0,
∴抛物线开口向上,
当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5)
(2)
解:抛物线的对称轴为x=1,
∴﹣ ![]() =﹣
=﹣ ![]() =1,
=1,
解得b=﹣1,
故抛物线的解析式为y=x2﹣2x﹣5;
图象如下:
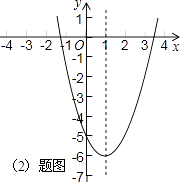
(3)
解:∵b>3,
∴抛物线的对称轴x=﹣ ![]() =﹣
=﹣ ![]() <﹣1,
<﹣1,
∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA,
∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得,
![]() ,
,
解得 ![]() ,
,
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;
[或:∵点B(﹣3,c)、P(﹣1,c),
∴BP的中点(﹣2,c)在抛物线的对称轴上,
∴﹣ ![]() =﹣
=﹣ ![]() =﹣2,解得b=5.]
=﹣2,解得b=5.]
【解析】(1)根据a值大于0,判断抛物线的开口向上,令x=0求出函数值y,就是抛物线与y轴的交点坐标;(2)根据对称轴解析式列式求出b的值,从而得到抛物线解析式,再根据抛物线与坐标轴的交点与顶点坐标作出草图即可;(3)先根据b>3判断出点P在对称轴的左侧,然后根据BP=2PA求出点B的坐标,然后把点P、B的坐标代入抛物线解析式,利用待定系数法求出b、c的值,即可写出该抛物线对应的二次函数解析式.[或者根据点BP的中点在抛物线的对称轴上,利用对称轴解析式列式进行计算求解b的值.]
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是BC上的点.求证:BD2+CD2=2AD2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧
 上的一个动点,弦AB,CP相交于点D.
上的一个动点,弦AB,CP相交于点D. 
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
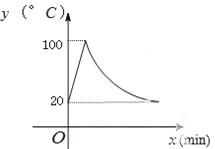
(1) 分别求出直线及双曲线的解析式.
(2) 学生在每次温度升降过程中能喝到50℃以上水的时间有多长?
(3) 若某天上午六点饮水机自动接通电源,问学生上午第一节下课时(8:15)能喝到超过50℃的水吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求
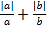 的值.
的值.(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则
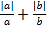 =
=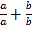 =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则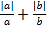 =
=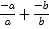 =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以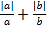 的值为2或﹣2.
的值为2或﹣2.(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求
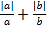 的值;
的值;(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
相关试题

