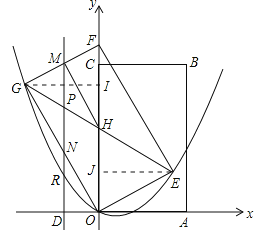
【题目】如图,矩形OABC的顶点A(2,0)、C(0,2![]() ).将矩形OABC绕点O逆时针旋转30°.得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.
).将矩形OABC绕点O逆时针旋转30°.得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.

(1)若抛物线l经过G、O、E三点,求l的解析式;
(2)如果四边形OHMN为平行四边形,求点D的坐标;
(3)在(1)(2)的条件下,直线MN与抛物线l交于点R,动点Q在抛物线l上且在R、E两点之间(不含点R、E)运动,设△PQH的面积为s,当![]() <s≤
<s≤![]() 时,确定点Q的横坐标的取值范围.
时,确定点Q的横坐标的取值范围.
参考答案:
【答案】(1)y=![]() .(2)D(-
.(2)D(-![]() ,0).(3)-
,0).(3)-![]() <x<
<x<![]() .
.
【解析】
试题解析:(1)求解析式一般采用待定系数法,通过函数上的点满足方程求出.
(2)平行四边形对边平行且相等,恰得MN为![]() OF,即为中位线,进而横坐标易得,D为x轴上的点,所以纵坐标为0.
OF,即为中位线,进而横坐标易得,D为x轴上的点,所以纵坐标为0.
(3)已知S范围求横坐标的范围,那么表示S是关键.由PH不为平行于x轴或y轴的线段,所以考虑利用过动点的平行于y轴的直线切三角形为2个三角形的常规方法来解题,此法底为两点纵坐标得差,高为横坐标的差,进而可表示出S,但要注意,当Q在O点右边时,所求三角形为两三角形的差.得关系式再代入![]() <s≤
<s≤![]() ,求解不等式即可.另要注意求解出结果后要考虑Q本身在R、E之间的限制.
,求解不等式即可.另要注意求解出结果后要考虑Q本身在R、E之间的限制.
试题解析:(1)如图1,过G作GI⊥CO于I,过E作EJ⊥CO于J,
∵A(2,0)、C(0,2![]() ),
),
∴OE=OA=2,OG=OC=2![]() ,
,
∵∠GOI=30°,∠JOE=90°-∠GOI=90°-30°=60°,
∴GI=sin30°![]() GO=
GO=![]() ×2
×2![]() =
=![]() ,
,
IO=cos30°![]() GO=
GO=![]() ×2
×2![]() =3,
=3,
JE=cos30°![]() OE=
OE=![]() ×2=
×2=![]() ,
,
JO=sin30°![]() OE=
OE=![]() ×2=1,
×2=1,
∴G(-![]() ,3),E(
,3),E(![]() ,1),
,1),
设抛物线解析式为y=ax2+bx+c,
∵经过G、O、E三点,
∴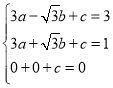 ,解得
,解得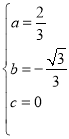 ,
,
∴y=![]() .
.
(2)∵四边形OHMN为平行四边形,
∴MN∥OH,MN=OH,
∵OH=![]() OF,
OF,
∴MN为△OGF的中位线,
∴xD=xN=![]() xG=-
xG=-![]() ,
,
∴D(-![]() ,0).
,0).
(3)设直线GE的解析式为y=kx+b,
∵G(-![]() ,3),E(
,3),E(![]() ,1),
,1),
∴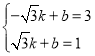 ,
,
解得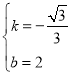 ,
,
∴y=-![]() x+2.
x+2.
∵Q在抛物线y=![]() 上,
上,
∴设Q的坐标为(x,![]() ),
),
∵Q在R、E两点之间运动,
∴-![]() <x<
<x<![]() .
.
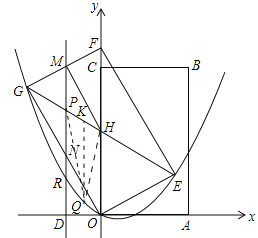
①当-![]() <x<0时,
<x<0时,
如图2,连接PQ,HQ,过点Q作QK∥y轴,交GE于K,则K(x,-![]() x+2),
x+2),
∵S△PKQ=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xQ-xP),
(xQ-xP),
S△HKQ=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xH-xQ),
(xH-xQ),
∴S△PQH=S△PKQ+S△HKQ=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xQ-xP)+
(xQ-xP)+![]()
![]() (yK-yQ)
(yK-yQ)![]() (xH-xQ)
(xH-xQ)
=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xH-xP)=
(xH-xP)=![]() × [-
× [-![]() x+2-(
x+2-(![]() x2-
x2-![]() x)] ×[0-(-
x)] ×[0-(-![]() )]=-
)]=-![]() x2+
x2+![]() .
.
②当0≤x<![]() 时,
时,
如图3,连接PQ,HQ,过点Q作QK∥y轴,交GE于K,则K(x,-![]() x+2),
x+2),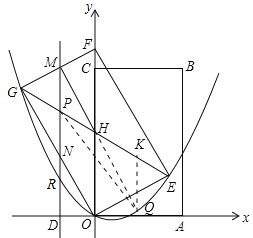
同理 S△PQH=S△PKQ-S△HKQ=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xQ-xP)-
(xQ-xP)-![]()
![]() (yK-yQ)
(yK-yQ)![]() (xQ-xH)
(xQ-xH)
=![]()
![]() (yK-yQ)
(yK-yQ)![]() (xH-xP)=-
(xH-xP)=-![]() x2+
x2+![]() .
.
综上所述,S△PQH=-![]() x2+
x2+![]() .
.
∵![]() <s≤
<s≤![]() ,
,
当S=![]() 时,对应的x=-
时,对应的x=-![]() 和
和![]() ,
,
因此由S=-![]() x2+
x2+![]() 的图象可得-
的图象可得-![]() <x<
<x<![]() 时满足
时满足![]() <s≤
<s≤![]() ,
,
∵-![]() <x<
<x<![]() ,
,
∴-![]() <x<
<x<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形的两边长分别是4、8,那么它的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(a﹣4b)(a+b)+3ab.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)15°30′=_______;
(2)25.35°=________;
(3)6.75°=_______;
(4)36°48′36″=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC,△ADE为等腰直角三角形,∠ACB=∠AED=90°.(1)如图1,点E在AB上,点D与C重合,F为线段BD的中点.则线段EF与FC的数量关系是 ;∠EFD的度数为 ;
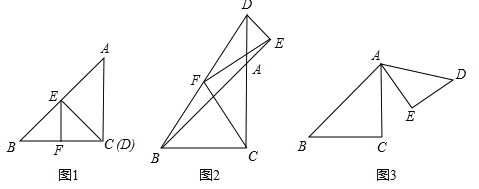
(2)如图2,在图1的基础上,将△ADE绕A点顺时针旋转到如图2的位置,其中D、A、C在一条直线上,F为线段BD的中点.则线段EF与FC是否存在某种确定的数量关系和位置关系?证明你的结论;
(3)若△ADE绕A点任意旋转一个角度到如图③的位置,F为线段BD的中点,连接EF、FC,请你完成图3,请猜想线段EF与FC的关系,并验证你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
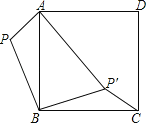
A.105° B.112.5° C.120° D.135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( ).
A.②③ B.③ C.①② D.①
相关试题

