搜索
【题目】如果等腰三角形的两边长分别是4、8，那么它的周长是 ．
参考答案：
【答案】20
【解析】解：∵等腰三角形有两边分别分别是4和8， ∴此题有两种情况：
①4为底边，那么8就是腰，则等腰三角形的周长为4+8+8=20，
②8底边，那么4是腰，4+4=8，所以不能围成三角形应舍去．
∴该等腰三角形的周长为20，
故答案为：20
解决本题要注意分为两种情况4为底或8为底，还要考虑到各种情况是否满足三角形的三边关系来进行解答．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列图形一定相似的是（ ）
A. 两个矩形B. 两个等腰梯形
C. 有一个内角相等的两个菱形D. 对应边成比例的两个四边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列线段中能围成三角形的是（ ）
A. 1，2，3B. 4，5，6C. 5，6，11D. 7，10，18
-
科目： 来源： 题型：
查看答案和解析>>【题目】写出点M（﹣2，3）关于x轴对称的点N的坐标 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：（a﹣4b）（a+b）+3ab．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
(1)15°30′＝_______；
(2)25.35°＝________；
(3)6.75°＝_______；
(4)36°48′36″＝_________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形OABC的顶点A（2，0）、C（0，2
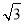）．将矩形OABC绕点O逆时针旋转30°．得矩形OEFG，线段GE、FO相交于点H，平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D，连结MH．
（1）若抛物线l经过G、O、E三点，求l的解析式；
（2）如果四边形OHMN为平行四边形，求点D的坐标；
（3）在（1）（2）的条件下，直线MN与抛物线l交于点R，动点Q在抛物线l上且在R、E两点之间（不含点R、E）运动，设△PQH的面积为s，当
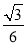＜s≤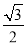
时，确定点Q的横坐标的取值范围．
相关试题
