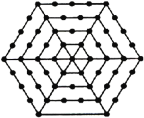
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | … |
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.
参考答案:
【答案】(1)12、18、24;(2)6(n-1)(n≥2);(3)17;(4)没有;(5)![]() .
.
【解析】
(1)根据题目中的图形和题意,可以将表格中的数据补充完整;
(2)根据(1)中填写的表格找规律即可得出答案;
(3)根据(2)中得出的第n层所对应的点数等于96,求出n即可得出答案;
(4)根据(2)中得出的第n层所对应的点数等于100,看求出的n是否为整数即可得出答案;
(5)根据(2)中得出的第n层所对应的点数,把每一层所对应的点数相加即可得出答案.
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | … | |
该层对应的点数 | 1 | 6 | 12 | 18 | 24 | … |
(2)根据(1)中所填表格可发现规律,
第n层所对应点数为:6(n-1)(n≥2);
(3)6(n-1)=96,
n=17;
(4)6(n-1)=100,
n=![]() ,
,
所以没有一层,它的点数为100个;
(5)1+6×1+6×2+6×3+6×4+...+6×(n-1)
=1+6×(1+2+3+4+…+n-1)
=1+![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了出行方便,现在很多家庭都购买了小汽车.又由于能源紧张和环境保护,石油的市场价格常常波动.为了在价格的波动中尽可能减少损失,常常有两种加油方案.
方案一:每次加50元的油.方案二:每次加50升的油.
请同学们以2次加油为例(第一次油价为a元/升,第二次油价为b元/升,a>0,b>0且a≠b),计算这两种方案中,哪种加油方案更实惠便宜(平均单价小的便宜)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价现在的售价为每箱36元,每月可销售60箱市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围;
(2)市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元? -
科目: 来源: 题型:
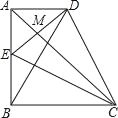
查看答案和解析>>【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习多项式乘以多项式时发现:(
 x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为: x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(
 x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG、DE.
 n
n
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形OE’F’G’,如图2.
<360°)得到正方形OE’F’G’,如图2.
①在旋转过程中,当∠OAG’是直角时,求 的度数;
的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF’长的最大值和此时 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
相关试题

