【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
参考答案:
【答案】(1)﹣7;(2)63.5;(3)a=﹣3;(4)2018.
【解析】
多项式乘多项式就是把一个多项式每一项去乘另一个多项式,在把所得积相加,根据题干提示,我们可以根据题目要求可以选择性求出一次项和二次项以及多项的系数.
(1)中求一次项系数,含有一次项的有x,3x,4x,这三个中依次选出其中一个在与另外两项中的常数想乘最终积相加即可或者展开所有的式子得出一次项系数.
(2)中求二次项系数,含有未知数的为:![]() x、2x、5x,选出其中两个在与另一个括号的常数相 乘,最后所得的积相加或者展开所有的式子得出一次项系数
x、2x、5x,选出其中两个在与另一个括号的常数相 乘,最后所得的积相加或者展开所有的式子得出一次项系数
(3)先根据(1)(2)所求方法求出一次项系数,最后用a表示,列出等式,求出a
(4)根据前三问的规律可以计算出第四问的值
解:(1)由题意得:
一次项系数是:1×2×(﹣3)+1×3×(﹣3)+1×2×4=﹣7;
(2)由题干材料知:
二次项系数为:![]() ×2×(﹣4)+6×2×5+
×2×(﹣4)+6×2×5+![]() ×5×3=63.5;
×5×3=63.5;
(3)一次项系数为:
1×a×(﹣1)+1×(﹣3)×(﹣1)+1×a×2=0
∴a=﹣3
(4)通过题干以及前三问知:a2017=2018×1=2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价现在的售价为每箱36元,每月可销售60箱市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围;
(2)市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元? -
科目: 来源: 题型:
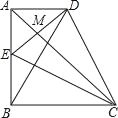
查看答案和解析>>【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
-
科目: 来源: 题型:
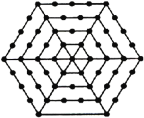
查看答案和解析>>【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数
1
2
3
4
5
…
该层对应的点数
1
6
…
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG、DE.
 n
n
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形OE’F’G’,如图2.
<360°)得到正方形OE’F’G’,如图2.
①在旋转过程中,当∠OAG’是直角时,求 的度数;
的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF’长的最大值和此时 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是( )
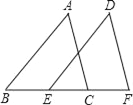
A. AB=DEB. AC=DFC. ∠A=∠DD. ∠ACB=∠F
相关试题

