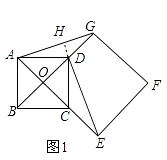
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG、DE. n
n
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< ![]() <360°)得到正方形OE’F’G’,如图2.
<360°)得到正方形OE’F’G’,如图2.
①在旋转过程中,当∠OAG’是直角时,求 ![]() 的度数;
的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF’长的最大值和此时 ![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
参考答案:
【答案】
(1)证明:如图1,延长ED交AG于点H,
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∵OG=OE,
在△AOG和△DOE中,
 ,
,
∴△AOG≌△DOE,
∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,
∴∠GAO+∠DEO=90°,
∴∠AHE=90°,
即DE⊥AG;
(2)解:①在旋转过程中,∠OAG′成为直角有两种情况:
(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD= ![]() OG=
OG= ![]() OG′,
OG′,
∴在Rt△OAG′中,sin∠AG′O= ![]() =
= ![]() ,
,
∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,
∴OD∥AG′,
∴∠DOG′=∠AG′O=30°,
即α=30°;
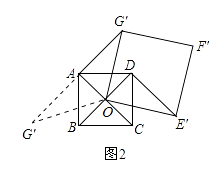
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,
∴α=180°30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②如图3,当旋转到A. O、F′在一条直线上时,AF′的长最大,
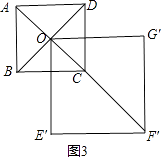
∵正方形ABCD的边长为1,
∴OA=OD=OC=OB= ![]() ,
,
∵OG=2OD,
∴OG′=OG= ![]() ,
,
∴OF′=2,
∴AF′=AO+OF′= ![]() +2,
+2,
∵∠COE′=45°,
∴此时α=315°
【解析】(1)延长ED交AG于点H,根据正方形的性质得出得出OA=OD,OG=OE,再证△AOG≌△DOE,得出∠AGO=∠DEO,根据等量代换证明结论。
(2)①根据题意和锐角正弦的概念以及特殊角的三角函数值得到∠AG′O=30°,分两种情况求出α的度数。
②根据正方形的性质分别求出OA和OF的长,根据旋转变换的性质求出AF′长的最大值和此时α的度数。
-
科目: 来源: 题型:
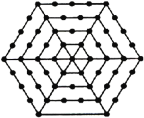
查看答案和解析>>【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数
1
2
3
4
5
…
该层对应的点数
1
6
…
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习多项式乘以多项式时发现:(
 x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为: x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(
 x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是( )
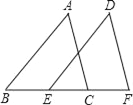
A. AB=DEB. AC=DFC. ∠A=∠DD. ∠ACB=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

相关试题

