【题目】如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6 ． 其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（　　）
A.86
B.64
C.54
D.48

参考答案：

【答案】A
【解析】解：如图1，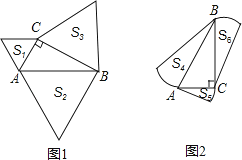

S1= AC2 ， S2= BC2 ， S3= AB2 ．
∵AB2=AC2+BC2 ，
∴S1+S2=AC2+BC2=AB2=S3 ，
如图2，S4=S5+S6 ，
∴S3+S4=16+45+11+14=86．
故选A．
分别用AB、BC和AC表示出 S1、S2、S3 ， 然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系．同理，得出S4、S5、S6的关系．本题考查了勾股定理、等边三角形的性质．勾股定理：如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2 ．

关闭