【题目】如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为 . 
参考答案:
【答案】9π
【解析】解:连接PA、PD,过点P作PE垂直AB于点E,延长PE交CD于点F,如图所示.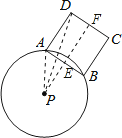
∵AB是⊙P上一弦,且PE⊥AB,
∴AE=BE= ![]() AB=3.
AB=3.
在Rt△AEP中,AE=3,PA=5,∠AEP=90°,
∴PE= ![]() =4.
=4.
∵四边形ABCD为正方形,
∴AB∥CD,AB=BC=6,
又∵PE⊥AB,
∴PF⊥CD,
∴EF=BC=6,DF=AE=3,PF=PE+EF=4+6=10.
在Rt△PFD中,PF=10,DF=3,∠PFE=90°,
∴PD= ![]() .
.
∵若AB边绕点P旋转一周,则CD边扫过的图形为以PF为内圆半径、以PD为外圆半径的圆环.
∴S=πPD2﹣πPF2=109π﹣100π=9π.
故答案为:9π.
连接PA、PD,过点P作PE垂直AB于点E,延长AE交CD于点F,根据垂径定理可得出AE=BE= ![]() AB,利用勾股定理即可求出PE的长度,再根据平行线的性质结合正方形的性质即可得出EF=BC=AB,DF=AE,再通过勾股定理即可求出线段PD的长度,根据边与边的关系可找出PF的长度,分析AB旋转的过程可知CD边扫过的区域为以PF为内圆半径、以PD为外圆半径的圆环,根据圆环的面积公式即可得出结论.本题考查了垂径定理、勾股定理、平行线的性质以及圆环的面积公式,解题的关键是分析出CD边扫过的区域的形状.本题属于中档题,难度不大,但稍显繁琐,解决该题型题目时,结合AB边的旋转,找出CD边旋转过程中扫过区域的形状是关键.
AB,利用勾股定理即可求出PE的长度,再根据平行线的性质结合正方形的性质即可得出EF=BC=AB,DF=AE,再通过勾股定理即可求出线段PD的长度,根据边与边的关系可找出PF的长度,分析AB旋转的过程可知CD边扫过的区域为以PF为内圆半径、以PD为外圆半径的圆环,根据圆环的面积公式即可得出结论.本题考查了垂径定理、勾股定理、平行线的性质以及圆环的面积公式,解题的关键是分析出CD边扫过的区域的形状.本题属于中档题,难度不大,但稍显繁琐,解决该题型题目时,结合AB边的旋转,找出CD边旋转过程中扫过区域的形状是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )

A.86
B.64
C.54
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车公司调查阳光中学学生对其产品的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.
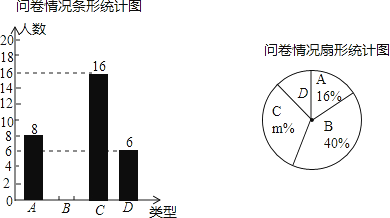
(1)本次问卷共随机调查了名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.

(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
相关试题

