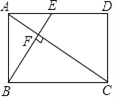
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△ABF:S四边形CDEF=2:5;④cos∠CAD=![]() .其中正确的结论有( ).
.其中正确的结论有( ).
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】A
【解析】∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∴∠EAC=∠ACB,
∵BE⊥AC,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CF=2AF,故②正确;
∵△AEF∽△CBF,
∴EF:BF=1:2,
∴S△AEF=![]() S△ABF,S△AEF=
S△ABF,S△AEF=![]() S△BCF,
S△BCF,
∴S△ABF:S四边形CDEF=2:5,故③正确;
∵cos∠CAD=![]() ,故④正确;
,故④正确;
故选:A
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣4=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,且该方程的两个根都是整数,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线y=
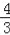 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
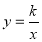 的图像与一次函数
的图像与一次函数 的图像的一个交点的横坐标是-3.
的图像的一个交点的横坐标是-3.(1)求
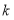 的值,并在指定坐标系中画出这两个函数的图像;
的值,并在指定坐标系中画出这两个函数的图像;(2)根据图像,直接写出使一次函数值大于反比例函数值时x的取值范围 .
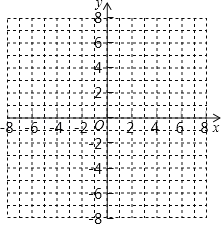
-
科目: 来源: 题型:
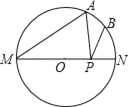
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=2a,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则 PA+PB的最小值为_____.(用含a的代数式表示)
-
科目: 来源: 题型:
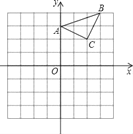
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1.
(2)点C1的坐标为( , ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
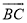 的长.
的长.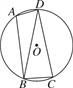
相关试题

