【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
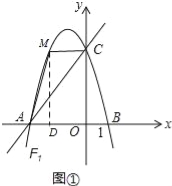
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
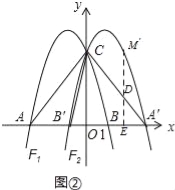
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4;(2)最大值为
x+4;(2)最大值为![]() ;M(﹣
;M(﹣![]() ,5);(3)(2,0)或(﹣
,5);(3)(2,0)或(﹣![]() ,0)
,0)
【解析】
试题分析:(1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)由于M在抛物线F1上,所以可设M(a,﹣![]() a2﹣
a2﹣![]() a+4),然后分别计算S四边形MAOC和S△BOC,过点M作MD⊥x轴于点D,则S四边形MAOC的值等于△ADM的面积与梯形DOCM的面积之和;(3)由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①
a+4),然后分别计算S四边形MAOC和S△BOC,过点M作MD⊥x轴于点D,则S四边形MAOC的值等于△ADM的面积与梯形DOCM的面积之和;(3)由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①![]() =
=![]() ;②
;②![]() =
=![]() .
.
试题解析:解:(1)令y=0代入y=![]() x+4,
x+4,
∴x=﹣3,
A(﹣3,0),
令x=0,代入y=![]() x+4,
x+4,
∴y=4,
∴C(0,4),
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣![]() ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+4,
x+4,
(2)如图①,设点M(a,﹣![]() a2﹣
a2﹣![]() a+4)
a+4)
其中﹣3<a<0
∵B(1,0),C(0,4),
∴OB=1,OC=4
∴S△BOC=![]() OBOC=2,
OBOC=2,
过点M作MP⊥x轴于点P,
∴MP=﹣![]() a2﹣
a2﹣![]() a+4,AP=a+3,OP=﹣a,
a+4,AP=a+3,OP=﹣a,
∴S四边形MAOC=![]() APMP+
APMP+![]() (MP+OC)OP
(MP+OC)OP
=![]() APMP+
APMP+![]() OPMP+
OPMP+![]() OPOC
OPOC
=![]() +
+![]()
=![]() +
+![]()
=![]() ×3(﹣
×3(﹣![]() a2﹣
a2﹣![]() a+4)+
a+4)+![]() ×4×(﹣a)
×4×(﹣a)
=﹣2a2﹣6a+6
∴S=S四边形MAOC﹣S△BOC
=(﹣2a2﹣6a+6)﹣2
=﹣2a2﹣6a+4
=﹣2(a+![]() )2+
)2+![]()
∴当a=﹣![]() 时,
时,
S有最大值,最大值为![]()
此时,M(﹣![]() ,5);
,5);
(3)如图②,由题意知:M′(![]() ),
),
∴AB′=2,
设直线A′C的解析式为:y=kx+b,
把A′(3,0)和C(0,4)代入y=kx+b,
得:![]() ,
,
∴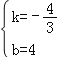
∴y=﹣![]() x+4,
x+4,
令x=![]() 代入y=﹣
代入y=﹣![]() x+4,
x+4,
∴y=2
∴![]()
由勾股定理分别可求得:AC=5,DA′=![]()
设P(m,0)
当m<3时,
此时点P在A′的左边,
∴∠DA′P=∠CAB′,
当![]() =
=![]() 时,△DA′P∽△CAB′,
时,△DA′P∽△CAB′,
此时,![]() =
=![]() (3﹣m),
(3﹣m),
解得:m=2,
∴P(2,0)
当![]() =
=![]() 时,△DA′P∽△B′AC,
时,△DA′P∽△B′AC,
此时,![]() =
=![]() (3﹣m)
(3﹣m)
m=﹣![]() ,
,
∴P(﹣![]() ,0)
,0)
当m>3时,
此时,点P在A′右边,
由于∠CB′O≠∠DA′E,
∴∠AB′C≠∠DA′P
∴此情况,△DA′P与△B′AC不能相似,
综上所述,当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是( )
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)若将线段AB绕点O逆时针旋转90°得到线段A1B1,试在图中画出线段A1B1.
(2)若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2.
(3)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某学校开展“远是君山,磨砺意志,保护江豚,爱鸟护鸟”为主题的远足活动.已知学校与君山岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
-
科目: 来源: 题型:
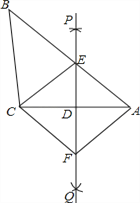
查看答案和解析>>【题目】如图,在△ABC中, PQ是CA的垂直平分线, CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两名同学在调查时使用下面两种提问方式,你认为哪一种更好些( )
A. 难道你不认为科幻片比武打片更有意思吗?
B. 你更喜欢哪一类电影 ——科幻片还是武打片?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两组数据:a1,a2,a3,a4,a5和a1-1,a2-1,a3-1,a4-1,a5-1,下列判断中错误的是( )
A. 平均数不相等,方差相等 B. 中位数不相等,标准差相等
C. 平均数相等,标准差不相等 D. 中位数不相等,方差相等
相关试题

