【题目】如图,△ABC中,∠BAC的内角平分线与外角平分线分别交BC及BC的延长线于点P、Q.
(1)求∠PAQ的大小;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
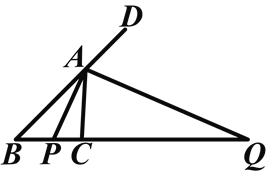
参考答案:
【答案】见解析
【解析】
(1)由角平分线的性质及∠BAD为平角直接可得;(2)由于线段PM、CM、BM在同一条直线上,所以必须把某条线段转化为另一相等的线段,构造相似三角形,因此,可证PM=AM,从而证明△ACM与△ABM相似即可.
解:
(1)∵AP平分∠BAC,∴![]() ,
,
又∵AQ平分∠CAD,∴![]() .
.
∴![]() .
.
又∵∠BAC+∠CAD=∠180°,∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:如图,连接AM,∵∠PAQ=90°,M是PQ的中点,∴PM=AM,∴∠APM=∠PAM.
∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,
∴∠B=∠CAM,∵∠AMC=∠BMA,
∴△ACM∽△BAM.
∴![]() .∴AM2=CM·BM,即PM2=CM·BM.
.∴AM2=CM·BM,即PM2=CM·BM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,﹣3),B(5,﹣1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
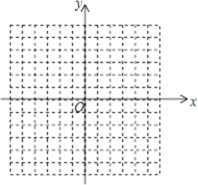
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于y轴对称的△A'B'C',并写出△A'B'C'各顶点坐标。
-
科目: 来源: 题型:
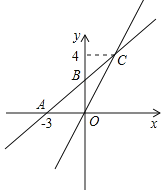
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=
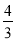 x的图象交点为C(m,4).
x的图象交点为C(m,4).(1)求一次函数y=kx+b的解析式;
(2)求△BOC的面积;
(3)若点D在第二象限,△DAB为等腰直角三角形,则点D的坐标为 .
-
科目: 来源: 题型:
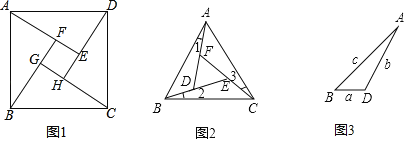
查看答案和解析>>【题目】问题背景:如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形.
类比探究:如图2,在正△ABC的内部,作∠1=∠2=∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象经过点(0,1),对称轴为直线x=﹣1,下列结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c>0;⑤c﹣a>1.其中,正确结论的个数为( )
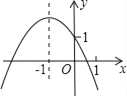
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
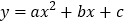 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①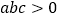 ;②
;②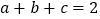 ;③
;③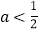 ;④
;④ .其中正确的结论是( )
.其中正确的结论是( )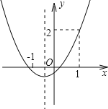
A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型超市投入15000元资金购进
 、
、 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:类别/单价
成本价(元/箱)
销售价(元/箱)
A品牌
20
32
B品牌
35
50
(1)该大型超市购进
 、
、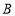 品牌矿泉水各多少箱?
品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?
相关试题

