【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

参考答案:
【答案】(1)过A,B两点的直线解析式为y=2x+3;
(2)△ABP的面积为![]() 或
或![]() .
.
【解析】
(1)设直线l的解析式为y=ax+b,把A、B的坐标代入求出即可;
(2)分为两种情况:①当P在x轴的负半轴上时,②当P在x轴的正半轴上时,求出AP,再根据三角形面积公式求出即可.
解:(1)设过A,B两点的直线解析式为y=ax+b(a≠0),
则根据题意,得 ,
,
解得:![]() ,
,
则过A,B两点的直线解析式为y=2x+3;
(2)设P点坐标为(x,0),依题意得x=±3,
∴P点坐标分别为P1(3,0),P2(﹣3,0),
![]() =
=![]() ,
,
![]() =
=![]() ,
,
故△ABP的面积为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,∠BAE=∠EAC,O是AC的中点,AD=DC=2,下面结论:①AC=2AB;②AB=
 ;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )
;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点A、C均在坐标轴上,且OA=4,OC=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC于点P,连接MP.

(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
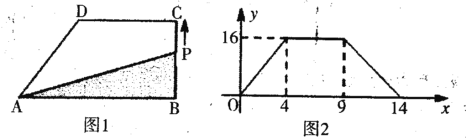
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)当点P运动的路程x=4时,△ABP的面积为y= ;
(2)求:线段AB的长;
(3)求:梯形ABCD的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】非负数
 满足
满足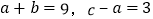 ,设
,设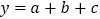 的最大值为
的最大值为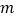 ,最小值为
,最小值为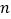 ,则
,则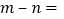 _______.
_______.
相关试题

