【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.

(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
参考答案:
【答案】(1)见解析;(2)AB=BC.
【解析】
(1)证明DB=EC. DB∥EC即可;
(2)矩形的判定方法有多种,可选择利用“对角线相等的平行四边形为矩形”来解决.
(1)证明:∵E是AC中点,
∴EC=![]() AC.
AC.
∵DB=![]() AC,
AC,
∴DB=EC.
又∵DB∥EC,
∴四边形DBCE是平行四边形.
(2)如图,连接AD,BE,
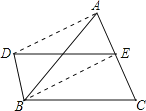
添加AB=BC.
理由:∵DB∥AE,DB=AE,
∴四边形DBEA是平行四边形.
∵BC=DE,AB=BC,
∴AB=DE.
∴ADBE是矩形.
故答案为:AB=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点A、C均在坐标轴上,且OA=4,OC=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC于点P,连接MP.

(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣
 ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

-
科目: 来源: 题型:
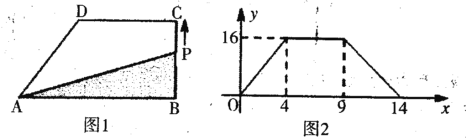
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)当点P运动的路程x=4时,△ABP的面积为y= ;
(2)求:线段AB的长;
(3)求:梯形ABCD的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】非负数
 满足
满足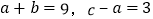 ,设
,设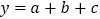 的最大值为
的最大值为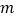 ,最小值为
,最小值为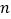 ,则
,则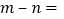 _______.
_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B是反比例函数y=
 (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
相关试题

