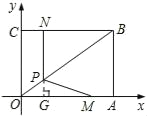
【题目】如图,在直角坐标系中,矩形OABC的顶点A、C均在坐标轴上,且OA=4,OC=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC于点P,连接MP.

(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
参考答案:
【答案】(1)B点坐标为(4,3).点P的坐标为(x,![]() x);(2)当x=2时,S有最大值,最大值为
x);(2)当x=2时,S有最大值,最大值为![]() ;(3) M的坐标为(
;(3) M的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)根据矩形OABC中OA=4,OC=3以及矩形的性质,得出B点坐标,再由PG∥AB,得出△OPG∽△OBA,利用相似三角形对应边成比例得出P点坐标;
(2)利用PG以及OM的长表示出△OMP的面积,再根据二次函数的性质求出最大值即可;
(3)△OMP是等腰三角形时,分三种情况:①PO=PM;②OP=OM;③OM=PM.画出图形,分别求出即可.
试题解析:(1)∵矩形OABC中,OA=4,OC=3,
∴B点坐标为(4,3).
如图,延长NP,交OA于点G,则PG∥AB,OG=CN=x.
∵PG∥AB,
∴△OPG∽△OBA,
∴![]() ,即
,即![]() ,解得PG=
,解得PG=![]() x,
x,
∴点P的坐标为(x,![]() x);
x);
(2)∵在△OMP中,OM=4-x,OM边上的高为![]() x,
x,
∴S=![]() (4-x)
(4-x)![]() x=-
x=-![]() x2+
x2+![]() x,
x,
∴S与x之间的函数表达式为S=-![]() x2+
x2+![]() x(0<x<4).
x(0<x<4).
配方,得S=-![]() (x-2)2+
(x-2)2+![]() ,
,
∴当x=2时,S有最大值,最大值为![]() ;
;
(3)存在某一时刻,使△OMP是等腰三角形.理由如下:
①如备用图1,

若PO=PM,则OG=GM=CN=x,
即3x=4,解得:x=![]() ,
,
所以M(![]() ,0);
,0);
②如备用图2,

若OP=OM,则![]() =OM,
=OM,
即![]() x=4-x,解得:x=
x=4-x,解得:x=![]() ,
,
所以M(![]() ,0);
,0);
③如备用图3,

若OM=PM时,
∵PG=![]() x,GM=OM-OG=(4-x)-x=4-2x,
x,GM=OM-OG=(4-x)-x=4-2x,
∴PM2=PG2+GM2=(![]() x)2+(4-2x)2,
x)2+(4-2x)2,
∵OM=4-x,
∴(4-x)2=(![]() x)2+(4-2x)2,解得:x=
x)2+(4-2x)2,解得:x=![]() ,
,
所以,M(![]() ,0).
,0).
综上所述,M的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB.(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=
 ,求BC和BF的长.
,求BC和BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,∠BAE=∠EAC,O是AC的中点,AD=DC=2,下面结论:①AC=2AB;②AB=
 ;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )
;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣
 ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

-
科目: 来源: 题型:
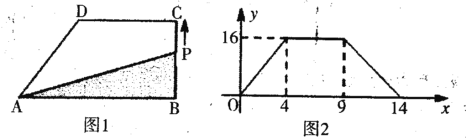
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)当点P运动的路程x=4时,△ABP的面积为y= ;
(2)求:线段AB的长;
(3)求:梯形ABCD的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
相关试题

