【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:

①AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
②AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等的有_____个.
参考答案:
【答案】3.
【解析】
根据条件能证明①②③中△ABD≌△A1B1D1(SAS),和△BCD≌△B1C1D1(AAS或ASA),从而利用全等三角形的性质与等式的性质得出两个四边形四条边对应相等,四个角对应相等,因而这两个四边形全等.
证明:①连接BD、B1D1.
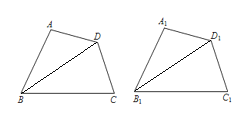
∵AB=A1B1,AD=A1D1,∠A=∠A1,
∴△ABD≌△A1B1D1.
∴BD= B1D1,∠ABD =∠A1B1D1,
∠ADB =∠A1 D1B1.
∵∠ABC =∠A1B1C1,
∴∠DBC =∠D1B1C1,
又∵∠C=∠C1,BD= B1D1,
∴△BCD≌△B1C1D1.
∴BC=B1C1,CD=C1D1,∠BDC=∠B1 D1C1,
∴∠ADC=∠A1D1C1.
∴四边形ABCD≌四边形A1B1C1D1;
②∵∠A=∠A1,∠B=∠B1,∠D=∠D1,
∴∠C=∠C1,
同①可证明②;
同②可证明③;
由④不能判定四边形ABCD和四边形A1B1C1D1全等,
∴能判定四边形ABCD和四边形A1B1C1D1全等的有3个:①②③.
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中, ,垂足为
,垂足为 ,
, ,
, ,
, 是
是 的中点.现有下列四个结论:①
的中点.现有下列四个结论:① ;②四边形
;②四边形 的面积等于
的面积等于 ;③
;③ ;④
;④ .其中正确结论的个数为( )
.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点O是边AB、AC垂直平分线的交点,点E是∠ABC、∠ACB角平分线的交点,若∠O+∠E=180°,则∠A=_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 为
为 边上的中线,过点
边上的中线,过点 作
作 于点
于点 ,过点
,过点 作
作 平行线,交
平行线,交 的延长线于点
的延长线于点 ,在延长线上截得
,在延长线上截得 ,连结
,连结 、
、 .若
.若 ,
, ,则四边形
,则四边形 的面积等于________.
的面积等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小华同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小丽同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).

(1)你能说出小华、小丽所折出的菱形的理由吗?
(2)请你通过计算,比较小华和小丽同学的折法中,哪种菱形面积较大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过
的中点,过 点作
点作 的平行线交
的平行线交 的延长线于点
的延长线于点 ,且
,且 ,连接
,连接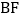 .
.
 与
与 有什么数量关系,并说明理由;
有什么数量关系,并说明理由; ①当
①当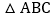 满足什么条件时,四边形
满足什么条件时,四边形 是矩形?并说明理由.
是矩形?并说明理由.②当
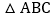 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?并说明理由.
是菱形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,

(1)请你利用直尺和圆规完成如下操作:
①作△ABC的角平分线AD;
②作边AB的垂直平分线EF,EF与AD相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(2)线段PA,PB,PC之间的数量关系是 ;请说明理由.
(3)若∠ABC=70°,求∠BPC的度数.
相关试题

