Question

【题目】如图，△ABC中，AB＝AC，

(1)请你利用直尺和圆规完成如下操作：

①作△ABC的角平分线AD；

②作边AB的垂直平分线EF，EF与AD相交于点P；

③连接PB，PC．

请你观察图形解答下列问题：

（2）线段PA，PB，PC之间的数量关系是　 　；请说明理由．

（3）若∠ABC＝70°，求∠BPC的度数．

Answer 1

【答案】（1）见解析；（2）PA=PB=PC，理由见解析；（3）80°．

【解析】

（1）利用基本作图作角平分线AD和AB的垂直平分线，它们相交于P点；

（2）根据线段的垂直平分线的性质可得：PA=PB=PC；
（3）根据等腰三角形的性质得：∠ABC=∠ACB=70°，由三角形的内角和得：∠BAC=180°-2×70°=40°，由角平分线定义得：∠BAD=∠CAD=20°，最后利用三角形外角的性质可得结论．

解：（1）如图，AD、EF 、点P为所作；

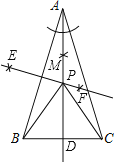
（2）PA=PB=PC，理由：
∵AB=AC，AD平分∠BAC，
∴AD是BC的垂直平分线，
∴PB=PC，
∵EP是AB的垂直平分线，
∴PA=PB，
∴PA=PB=PC；
故答案为：PA=PB=PC；
（3）∵AB=AC，
∴∠ABC=∠ACB=70°，
∴∠BAC=180°-2×70°=40°，
∵AM平分∠BAC，
∴∠BAD=∠CAD=20°，
∵PA=PB=PC，
∴∠ABP=∠BAP=∠ACP=20°，
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°．