Question

【题目】如图，在菱形中，，垂足为，，，是的中点．现有下列四个结论：①；②四边形的面积等于；③；④．其中正确结论的个数为（ ）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】

设DE=3k， AE=4k，根据勾股定理求得AD=5k，BE=k，从而求出边长及高，计算面积，可得①②正确；连接BD、AC，根据勾股定理可求对角线BD的长，再利用菱形面积的两种表示法求得AC的长，即可得③正确；作DH⊥BC于H点，则DH=DE，根据垂线段最短可得DH＜DF，所以DE＜DF，即可得④错误．

设DE=3k，则AE=4k，根据勾股定理求得AD=5k，

∴AD=AB=5k。

∴BE=AB-AE=5k-4k=k=1，

∴AB=5，DE=3．

故①正确；

S梯形DEBC=×（1+5）×3=9，

故②正确；

连接DB，

∵DE=3，EB=1，

∴DB=．

又∵SABCD=AB×DE=5×3=15，SABCD=×BD×AC，

∴15=× ×AC，

AC=3．

（AC+BD）（AC-BD）=AC2-BD2=（3）2-（）2=90-10=80．

故③正确；

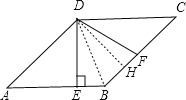
作DH⊥BC于H点．

∵DE⊥AB，DH⊥BC，∠ABD=∠CBD，

∴DE=DH．

又DH＜DF，

∴DE＜DF．故④错误．

所以①②③正确．

故选C．