Question

【题目】已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．

（1）发现：如图1，当E点旋转到DA的延长线上时，△ABE与△ADG的面积关系是：；
（2）引申：当正方形AEFG旋转任意一个角度时，△ABE与△ADG的面积关系是：；
（3）如图3，四边形ABMN、四边形DEAC、四边形BFGC均为正方形，则S△ABC、S△AEN、S△BMF、S△DCG的关系是；
（4）运用：某小区中有一块空地，要在其中建三个正方形健身场所（如图3），其余空地修成草坪．若已知其中一个正方形的边长为5m，另一个正方形的边长为4m，则草坪的最大面积是 ．

Answer 1

【答案】
（1）△ABE的面积=△ADG的面积
（2）△ABE的面积=△ADG的面积
（3）S△ABC=S△AEN=S△BMF=S△DCG
（4）30m2
【解析】解：（1）∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E点旋转到DA的延长线上
∴AE=AG，AB=AD，∠EAB=∠GAD=90°，
在△ABE和△ADG中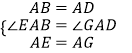
∴△ABE≌△ADG（SAS），
∴△ABE的面积=△ADG的面积；
所以答案是：△ABE的面积=△ADG的面积；
⑵结论仍然成立．理由如下：
作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图所示，
∵∠PAD=90°，∠EAG=90°，
∴∠PAE=∠GAH，
在△AHG和△AEP中， ，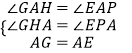
∴△AHG≌△AEP（AAS），
∴GH=BP，
∵△ABE的面积= EPAB，△ADG的面积= GHAD，
∴△ABE的面积=△ADG的面积；
所以答案是：△ABE的面积=△ADG的面积；
⑶由（2）得：S△ABC=S△AEN=S△BMF=S△DCG ，
所以答案是：S△ABC=S△AEN=S△BMF=S△DCG ，
⑷∵AB=5m，AC=4m，
∴△ABC的面积= ×5×4×sin∠BAC=10sin∠BAC，
当sin∠BAC=1时，△ABC的面积的最大值为10，
根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=3×10=30m2 ．
所以答案是：30m2 ．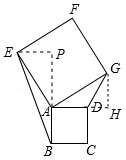

【考点精析】认真审题，首先需要了解正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)，还要掌握锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数)的相关知识才是答题的关键．